Skip to content

Latest commit

 

History

History
460 lines (329 loc) · 25.8 KB

practical_multivariable_linreg_gradient.md

File metadata and controls

460 lines (329 loc) · 25.8 KB
Raw

প্র্যাক্টিক্যাল মাল্টিভ্যারিয়েবল লিনিয়ার রিগ্রেশন : গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদমের রকমফের

গত পর্বে আমরা দেখেছিলাম সিঙ্গেল ভ্যারিয়েবল লিনিয়ার রিগ্রেশনের ফরমুলা ও পাইথনে ইম্প্লিমেন্টেশন। এই পর্বে দেখব মাল্টিভ্যারিয়েবল বা মাল্টিফিচার বিশিষ্ট রিগ্রেশন সমস্যা কীভাবে গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদমের মাধ্যমে সল্ভ করে। তবে এখানে সিনথেটিক ডেটা দিয়ে সবকিছু আলোচনা করা হবে। সিনথেটিক ডেটা হল কোন ম্যাথেমেটিক্যাল ফরমুলা ব্যবহার করে জেনারেট করা ডেটা। আজকের আলোচ্য কন্টেন্ট দেখা যাক।

গ্রেডিয়েন্ট ডিসেন্টের প্রকারভেদ জানা খুবই দরকারী। প্রায় সময়ই ফাংশন অপ্টিমাইজেশনের ক্ষেত্রে এই কথাগুলো বেশি পরিমাণে ব্যবহৃত হয়। সাধারণত লিনিয়ার রিগ্রেশনের ক্ষেত্রে এদের ব্যবহার দেখানো হয় না, কিন্তু সিম্পল লিনিয়ার মডেল দিয়েই অ্যালগরিদমগুলো ভাল বোঝা যায় তাই এখানে আলোচনা করা হল।

আলোচ্য বিষয়বস্তু:

  • গ্রেডিয়েন্ট ডিসেন্ট ফরমুলা ডিরাইভ করা
  • সিনথেটিক ডেটা প্রস্তুত করা
  • ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট (Batch Gradient Descent), স্টোক্যাস্টিক গ্রেডিয়েন্ট ডিসেন্ট (Stochastic Gradient Descent) ও মিনি-ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট (Mini-batch Gradient Descent) এর সুবিধা-অসুবিধা ও পাইথনে ইম্প্লিমেন্টেশন

লিনিয়ার রিগ্রেশনের জন্য গ্রেডিয়েন্ট ডিসেন্ট

গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদম বলে প্যারামিটারের ভ্যালু আপডেট করতে হবে এভাবে, $$ \theta_{j} := \theta_{j} - \alpha \frac{\partial J(\theta)}{\partial \theta_{j}} $$ যেখানে,

  • $$\theta$$ হল প্যারামিটার
  • $$j$$ দিয়ে বুঝাচ্ছে কততম প্যারামিটার
  • $$\alpha$$ হল লার্নিং রেট
  • $$J(\theta)$$ দিয়ে কস্ট ফাংশন বুঝানো হচ্ছে

$$ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m}\big(h_{\theta}(x^{(i)})-y^{(i)}\big)^{2} $$

আবার যেখানে

  • $$m$$ হচ্ছে রো সংখ্যা বা ডেটা কতগুলো আছে
  • $$h_{\theta}$$ হচ্ছে হাইপোথিসিস ফাংশন যেটা আমরা পরে ডিফাইন করব
  • $$y^{(i)}$$ হল ডেটাসেট এ দেয়া আউটপুট ভ্যালু
  • $$x^{(i)}$$ হল ইনপুট ডেটা

গ্রেডিয়েন্ট ডিসেন্ট ফরমুলেশন

আগে দেখানো হয়েছিল কীভাবে ম্যাট্রিক্সে কস্ট ক্যালকুলেট করে কিন্তু গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদমে কস্ট ফাংশনকে ডেরিভেটিভ করলে কী আসে সেটা দেখানো হয় নি। শুরু করা যাক।

লিনিয়ার রিগ্রেশনের হাইপোথিসিস সাধারণত এরকম হয়, $$ h_{\theta}(X) = \theta_{0}x_{0} + \theta_{1}x_{1}+\theta_{2}x_{2} $$ যেখানে, $$ X =x = \begin{bmatrix} x_{0}=1 \ x_{1} \ x_{2} \end{bmatrix} $$ যদি ইনপুটের ফিচার বা কলাম সংখ্যা হয় দুইটা। ডেটাসেট এ দুইটা ফিচার থাকলেও আমরা একস্ট্রা একটা কলাম $$1$$ সেট করে নেব। ম্যাট্রিক্সে ফরমুলেট করার জন্য এই $$1$$ এর গুরুত্ব অপরিসীম। (সাইড নোট: ইনপুট ভ্যারিয়েবলে মাঝে মাঝে $$X$$ বা $$x$$ হিসেবে লিখব, দুইটার মানে একই )

আমরা হাইপোথিসিস ফাংশনকে এভাবে আরও সংক্ষিপ্ত আকারে লিখতে পারি, $$ h_{\theta}(X) = \sum_{i=0}^{n}\theta_{i}x_{i} $$ ম্যাট্রিক্স আকারে, $$ h_{\theta}(X) = \theta^{T}X $$ বিখ্যাত ডেটাসেটটা আবার আনি,

বাড়ির আকার ( $$x_{1}$$) (sq-ft) ঘর সংখ্যা $$(x_{2})$$ বাড়ির দাম $$ y $$ (lac)
1200 5 120
1300 6 125
1400 7 130

এখানে, $$m=3$$ কারণ Row মাত্র তিনটা। এবং ফিচার দুইটা $$x_{1}, x_{2} $$ । যেহেতু $$x_{0}$$ সহ তিনটা তাই $$n=3$$

ডেটাসেট পাওয়ার পরে আমরা একস্ট্রা একটা ফিচার কলাম জুড়ে দিলে হবে এরকম,

$$x_{0}$$ বাড়ির আকার ( $$x_{1}$$) (sq-ft) ঘর সংখ্যা $$(x_{2})$$ বাড়ির দাম $$ y $$ (lac)
1 1200 5 120
1 1300 6 125
1 1400 7 130

$$\theta_{j} := \theta_{j} - \alpha \frac{\partial J(\theta)}{\partial \theta_{j}} $$

এই ফরমুলাতে আমাদের আগে বের করতে হবে, $$ \frac{\partial J(\theta)}{\partial \theta_{j}}$$ এটার মান কত। এটার মান বের করতে পারলে তারপর অ্যালগরিদমে বসিয়ে দিলেই হবে।

$$ \begin{align}

\frac{\partial J(\theta)}{\partial \theta_{j}}

&= \frac{\partial}{\partial \theta_{j}} \left[ \frac{1}{2m} \big(h_{\theta}(x) - y \big)^{2} \right]\

&= 2 \times \frac{1}{2m} \big(h_{\theta}(x) - y \big) \times \frac{\partial}{\partial \theta_{j} } \big(h_{\theta}(x) - y \big) \

&= \frac{1}{m} \times \big(h_{\theta}(x) - y \big) \times \frac{\partial}{\partial \theta_{j} } \left( \sum_{i=0}^{n}\theta_{i}x_{i} - y \right) \

&= \frac{1}{m} \times \big(h_{\theta}(x) - y \big) \times \left[ \frac{\partial}{\partial \theta_{j} } \left( \sum_{i=0}^{n}\theta_{i}x_{i} \right) - \frac{\partial y}{\partial \theta_{j} } \right] \

&= \frac{1}{m} \times \big(h_{\theta}(x) - y \big) \times \frac{\partial}{\partial \theta_{j} } \left( \sum_{i=0}^{n}\theta_{i}x_{i} \right) \end{align} $$

এখানে $$ \frac{\partial y}{\partial \theta_{j} } = 0$$ কারণ আউটপুট মানগুলো ভ্যারিয়েবল না, ধ্রুবক। তাই তাদের ডেরিভেটিভ নিলে ফলাফল আসবে শূন্য।

শেষের লাইনে একটি সমস্যা চলে এসেছে, সেটা হল হাইপোথিসিস ফাংশনের ডেরিভেটিভ কীভাবে বের করব। সেটা বের করার জন্য এক্সপ্রেশন আরও ভেঙ্গে লেখা যাক। $$ h_{\theta}(X) = \theta_{0}x_{0} + \theta_{1}x_{1}+\theta_{2}x_{2} $$ এই ফাংশনের পার্শিয়াল ডেরিভেটিভ আমরা $$\theta_{0}$$ এর সাপেক্ষে নিলে, (মনে আছে তো? পার্শিয়াল ডেরিভেটিভ যে ভ্যারিয়েবলের সাপেক্ষে নিব, সেটা বাদে সবাইকে ধ্রুবক হিসেবে গণনা করতে হবে।) $$ \frac{ \partial h_{\theta} (x) }{ \partial \theta_{0} } =

\left( x_{0} \times \frac{ \partial \theta_{0} }{ \partial \theta_{0}} + \theta_{0} \times \frac{ \partial x_{0} }{ \partial \theta_{0}} \right) +

\frac{ \partial }{ \partial \theta_{0}} ‌\left( \theta_{1}x_{1} \right) +

\frac{ \partial }{ \partial \theta_{0}} ‌\left( \theta_{2}x_{2} \right) $$ $$x_{0}, \theta_{1}x_{1}, \theta_{2}x_{2} $$ সবগুলোই ধ্রুবক $$\theta_{0}$$ এর কাছে, তাই $$ \frac{ \partial x_{0} }{ \partial \theta_{0}} = 0 \ \frac{ \partial }{ \partial \theta_{0}} ‌\left( \theta_{2}x_{2} \right) = 0 \ \frac{ \partial }{ \partial \theta_{0}} ‌\left( \theta_{1}x_{1} \right) = 0 $$ সুতরাং, $$ \frac{ \partial h_{\theta} (x) }{ \partial \theta_{0} } = x_{0} \times 1 = x_{0} $$ একইভাবে, $$ \frac{ \partial h_{\theta} (x) }{ \partial \theta_{1} } = x_{1} \ \frac{ \partial h_{\theta} (x) }{ \partial \theta_{2} } = x_{2} $$ জেনারেল ফর্মে, $$ \frac{ \partial h_{\theta} (x) }{ \partial \theta_{j} } =

\frac{ \partial }{ \partial \theta_{j}} \left( \sum_{i=0}^{n}\theta_{i}x_{i} \right) = x_{j} $$ এই সূত্র এবার কস্ট ফাংশনের ডেরিভেটিভে বসিয়ে পাওয়া যায়, $$ \frac{\partial J(\theta)}{\partial \theta_{j}} = \frac{1}{m} \times \big(h_{\theta}(x) - y \big) \times x_{j} $$ সিঙ্গেল প্যারামিটার আপডেটের গ্রেডিয়েন্ট ডিসেন্ট ফরমুলা সম্পূর্ণরূপে লিখলে, $$ \theta_{j} := \theta_{j} - \frac{\alpha}{m} \times \left( h_{\theta}(x^{(i)}) - y^{(i)} \right) \times x_{j}^{(i)} $$ অথবা এভাবেও লেখা যায় যদি আমি আউটপুট আগে বসাই, $$ \theta_{j} := \theta_{j} + \frac{\alpha}{m} \times \left( y^{(i)} - h_{\theta}(x^{(i)}) \right) \times x^{(i)}_{j} $$ নোটেশনে যাতে সমস্যা না হয় তাই আরেকবার ক্লিয়ার করা যাক,

  • $$x^{(i)}$$ কিন্তু ডেটাসেট এর $$i^{th}$$ $$row$$। অর্থাৎ উপরের উদাহরণ অনুযায়ী, $$2^{nd}$$ রো হল, $$ x^{(2)} = \begin{bmatrix} x_{0}^{(2)}=1 \ x_{1}^{(2)}= 1300 \ x_{2}^{(2)}= 6 \end{bmatrix} $$

  • $$x^{(i)}{j}$$ হল ডেটাসেট এর $$i^{th}$$ রো এর $$j^{th}$$ ফিচার। অর্থাৎ কিনা, $$x^{(2)}{2}=6$$

গ্রেডিয়েন্ট ডিসেন্ট ইম্প্লিমেন্টেশনে এই জিনিসটা খুবই গুরুত্বপূর্ণ। এই পর্যন্ত বুঝে থাকলে ইম্প্লিমেন্ট করা বা কোড বোঝা কোন ব্যাপারই না।

এই অ্যালগরিদম আমি তো কোন মডেলের উপর অ্যাপ্লাই করব, আর যে মডেল বিল্ড করব সেটা নির্ভর করবে ডেটাসেটের উপর। একটা নির্দিষ্ট কারণে আমি বাইরের ডেটাসেট ব্যবহার না করে সিনথেটিক্যালি ডেটাসেট প্রস্তুত করে সেটার উপর অ্যালগরিদম অ্যাপ্লাই করব।

সিনথেটিক ডেটা প্রস্তুতকরণ

ডেটা বিল্ড করার জন্য আমি একটা সিম্পল ফরমুলা ব্যবহার করব। সেটা হল এরকম, $$ y = 5 + 2 \times x_{1} +3\times x_{2} $$ যেখানে $$x_{1}, x_{2}$$ যেকোন ভ্যালু হতে পারে।

import numpy as np

def make_fake_data(x1, x2):
    # y = 5+2*x1+3*x2
    return float(5 + 2 * x1 + 3 * x2)

# first feature of input data, col - 1
feature_1 = np.array([float(i) for i in range(1, 21)])
# Second feature of input data, col - 2
feature_2 = np.array([float(i) for i in range(21, 41)])

# Output
y = np.array([
  make_fake_data(f1, f2)
  for f1, f2 in 
  zip(feature_1, feature_2)
])

বলাই বাহুল্য, এখানে $$x_{1}, x_{2}$$ হল ইনপুট ডেটার ফিচার বা কলাম। এই ফরমুলা দিয়ে বানানো ডেটাসেট হবে,

$$x_{1}$$ $$x_{2}$$ $$y$$
1 21 70
2 22 75
3 23 80
4 24 85
... ... ...
20 40 165

যেহেতু ইনপুট ফিচার দুইটা সেক্ষেত্রে আমাদের হাইপোথিসিস মডেল হবে, $$ h_{\theta}(X) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} $$

আমরা একে ম্যাট্রিক্সে ফরমুলেট না করে প্রথমে প্যারামিটারওয়াইজ ইটারেটিভ পদ্ধতিতে সল্ভ করব এবং পরে ম্যাট্রিক্স আকারে কিভাবে সল্ভ করে সেটা দেখব। তাই আমরা $$x_{0}=1$$ ফিচার ব্যবহার করিনি।

def predict(_theta_0, _theta_1, _theta_2, x1, x2):
    return _theta_0 + _theta_1 * x1 + _theta_2 * x2

গ্রেট, আমাদের হাইপোথিসিস ফাংশন আছে, ইনপুট ডেটা আর আউটপুট ডেটা আছে, আমাদের এখন অজানা $$\theta_{0}, \theta_{1}, \theta_{2}$$ এর মান বের করতে হবে শুধু।

কস্ট ক্যালকুলেশন ফাংশন:

প্রতি ইটারেশনে কস্ট কত সেটা ক্যালকুলেট করলে আমরা গ্রাফ প্লট করে দেখতে পারব এরর আসলেই কমছে কিনা। চিরাচরিত কস্ট ফাংশন, $$ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m}\big(h_{\theta}(x^{(i)})-y^{(i)}\big)^{2} $$ এটাকে এবার পাইথন ফাংশন আকারে লিখব,

def computeCost(t0, t1, t2, f1, f2, y):
    # Getting number of data 
    m = float(len(y))
    loss = []
    # Iterating over all of the data
    for i in range(len(y)):
        # Getting prediction using the parameter [t0, t1, t2]
        h = predict(t0, t1, t2, f1[i], f2[i])
        # Adding the losses to the list
        loss.append((h - y[i])**2)
        
    return (sum(loss) / (2 * m))

কস্ট বনাম ইটারেশন প্লট করার ফাংশন

এটা আমাদের কাজে আসবে তাই ফাংশন বানিয়ে নেয়াই ভাল,

def plot_cost_vs_iteration(costs):
    plt.plot([i for i in range(len(costs))], costs)
    plt.title("Cost vs Iteration")
    plt.xlabel("Iteration")
    plt.ylabel("Cost")
    plt.show()

গ্রেডিয়েন্ট ডিসেন্টের সাধারণত তিনরকম প্রকারভেদ দেখা যায়

  1. ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট (Batch Gradient Descent)
  2. স্টোক্যাস্টিক গ্রেডিয়েন্ট ডিসেন্ট (Stochastic Gradient Descent)
  3. মিনি-ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট (Mini-Batch Gradient Descent)

ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট

প্রথমে $$\theta_{0}, \theta_{1}, \theta_{2}$$ এর মান বের করব ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট দিয়ে, তারপর বাকি অ্যালগরিদম দিয়েও বের করব।

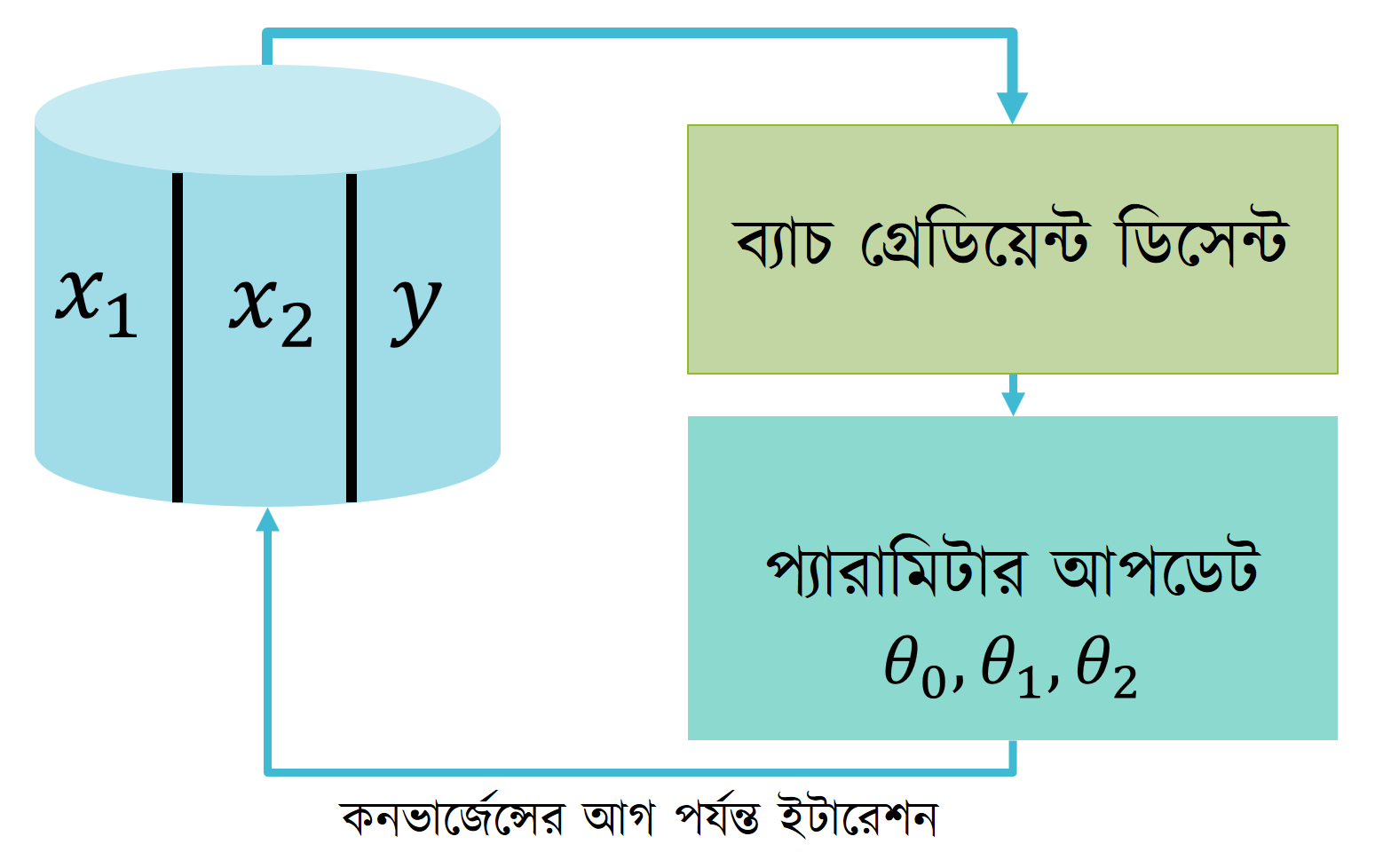
ব্যাচ গ্রেডিয়েন্ট ডিসেন্টের ফরমুলা, $$ Repeat \space Until \space Convergence \space { \

\theta_{j} := \theta_{j} + \alpha \sum_{i}^{m} \left( y^{(i)} - h_{\theta}(x^{(i)}) x \right) x_{j}^{(i)} \space\space\space (for \space every \space j) \\

} $$

# Parameters to be updated
_theta_0 = 0.0
_theta_1 = 0.0
_theta_2 = 0.0

# Data Length 
m = float(len(y))
        
# Epoch [No. of iterations]
epoch = 200

# Learning Rate
alpha = 0.001

# Costs
costs = []

# Batch Gradient Descent
for i in range(epoch):

    _theta_temp_0 = _theta_0 + (alpha / m) * sum([(y[k] - predict(_theta_0, _theta_1, _theta_2, feature_1[k], feature_2[k])) 
                                                     for k in range(len(y))
                                                 ])
    
    _theta_temp_1 = _theta_1 + (alpha / m) * sum([(y[k] - predict(_theta_0, _theta_1, _theta_2, feature_1[k], feature_2[k])) * feature_1[k] 
                                                     for k in range(len(y))
                                                 ])
    
    _theta_temp_2 = _theta_2 + (alpha / m) * sum([(y[k] - predict(_theta_0, _theta_1, _theta_2, feature_1[k], feature_2[k])) * feature_2[k] 
                                                     for k in range(len(y))
                                                 ])
    
    _theta_0 = _theta_temp_0
    _theta_1 = _theta_temp_1
    _theta_2 = _theta_temp_2
    
    # Calculating cost
    cost = computeCost(_theta_0, _theta_1, _theta_2, feature_1, feature_2, y)
    
    # Saving it to the list for future use
    costs.append(cost)
    
    # Printing cost after each epoch
    print("Cost: {}".format(cost))
    
# Plotting Cost vs Iteration Graph 
plot_cost_vs_iteration(costs)

এখানে কনভার্জেন্স শর্ত না বসিয়ে ইটারেশন দিয়ে লিমিট করে দেয়া হল।

কস্ট বনাম ইটারেশন প্লট

batch_cost

ব্যাচ গ্রেডিয়েন্ট ডিসেন্টে প্যারামিটার আপডেট

batch_grad_descent

ব্যাচ গ্রেডিয়েন্টের মূল অসুবিধা হল প্রতিবার প্যারামিটার ভ্যালু আপডেটের সময় বার বার সম্পূর্ণ ডেটাসেট ইটারেট করতে হয় এবং প্রতি প্যারামিটারের জন্য।

এই অসুবিধা দুর করার জন্য আরেকটি অ্যালগরিদম প্রায়ই ব্যবহার করা হয় যার নাম Stochastic Gradient Descent।

স্টোক্যাস্টিক গ্রেডিয়েন্ট ডিসেন্ট

Stochastic এর মানে হল কোন কিছু র‍্যান্ডমলি ডিটারমাইন করা। এখানে আমরা কস্ট ফাংশনকে অপ্টিমাইজ করব ডেটাসেট এর একেকটা রো নিয়ে।

আগে কোড দেখা যাক,

# Parameters to be updated
_theta_0 = 0.0
_theta_1 = 0.0
_theta_2 = 0.0

# Data Length 
m = float(len(y))
        
# Epoch [No. of iterations]
epoch = 10

# Learning Rate
alpha = 0.01

# Costs
costs = []

# Initializing Stochastic Gradient Descent
for i in range(epoch):
    
    # Iterate over all of the data 
    for j in range(len(y)):
        
        # Update theta_0 first
        _theta_0 = _theta_0 + (alpha / m) * (y[j] - predict(_theta_0, _theta_1, _theta_2, feature_1[j], feature_2[j]))
        
        # Use updated theta_0 to update theta_1
        _theta_1 = _theta_1 + (alpha / m) * (y[j] - predict(_theta_0, _theta_1, _theta_2, feature_1[j], feature_2[j])) * feature_1[j]
        
        # Again use theta_1 to update theta_2
        _theta_2 = _theta_2 + (alpha / m) * (y[j] - predict(_theta_0, _theta_1, _theta_2, feature_1[j], feature_2[j])) * feature_2[j]
    
    # Calculating cost
    cost = computeCost(_theta_0, _theta_1, _theta_2, feature_1, feature_2, y)
    
    # Saving it to the list for future use
    costs.append(cost)
    
    # Printing cost after each epoch
	print("Cost: {}".format(cost))
    
# Plotting Cost vs Iteration Graph 
plot_cost_vs_iteration(costs)

আমরা $$epoch$$ সম্পূর্ণ ডেটাসেট এ ব্যবহার না করে, প্রতি $$Row$$ ধরে প্যারামিটার আপডেট করি।

কস্ট বনাম ইটারেশন গ্রাফ

cost_vs_iter

স্টোক্যাস্টিক গ্রেডিয়েন্ট ডিসেন্ট কীভাবে কাজ করে?

sgd

মিনি ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট

ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট + স্টোক্যাস্টিক গ্রেডিয়েন্ট ডিসেন্ট = মিনি ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট! এর মানে, ব্যাচ গ্রেডিয়েন্ট ডিসেন্ট ও স্টোক্যাস্টিক গ্রেডিয়েন্ট ডিসেন্ট উভয় অ্যালগরিদমের ভাল জিনিসগুলো নিয়ে এই অ্যালগরিদম ডেভেলপ করা হয়েছে। ওভারশুট বা আন্ডারশুট সমস্যা ও কম্পিউটেশনাল কম্প্লেক্সিটির মধ্যে $$Trade-off$$ করার জন্যই মূলত এর উৎপত্তি।

কোড ও আউটপুট দেখা যাক।

# Parameters to be updated
_theta_0 = 0.0
_theta_1 = 0.0
_theta_2 = 0.0

# Data Length 
m = float(len(y))
        
# Epoch [No. of iterations]
epoch = 20

# Learning Rate
alpha = 0.01

# Costs
costs = []

# Mini Batch Gradient Descent
mini_batch_size = 5
mini_batches = int(m / mini_batch_size)

n = 0

for i in range(epoch):
    for batch in range(1, mini_batches + 1):
        n = batch * mini_batch_size
        for j in range(n):
            _theta_0 = _theta_0 + (alpha / m) * (y[j] - predict(_theta_0, _theta_1, _theta_2, feature_1[j], feature_2[j]))
            _theta_1 = _theta_1 + (alpha / m) * (y[j] - predict(_theta_0, _theta_1, _theta_2, feature_1[j], feature_2[j])) * feature_1[j]
            _theta_2 = _theta_2 + (alpha / m) * (y[j] - predict(_theta_0, _theta_1, _theta_2, feature_1[j], feature_2[j])) * feature_2[j]
    
    # Calculating cost
    cost = computeCost(_theta_0, _theta_1, _theta_2, feature_1, feature_2, y)
    
    # Saving it to the list for future use
    costs.append(cost)
    
    # Printing cost after each epoch
    print("Cost: {}".format(cost))
    
# Plotting Cost vs Iteration Graph 
plot_cost_vs_iteration(costs)

কস্ট বনাম ইটারেশন গ্রাফ

mini_batch_cost

মিনি ব্যাচে ডেটাসেট ভাগ করা

এখানে রো হচ্ছে ২০ টা, একে আমি ৫টি ব্যাচে ভাগ করেছি তাই প্রতি ব্যাচে রো সংখ্যা বা ডেটা সংখ্যা হল ৪।

অভারঅল ধারণা নেয়ার জন্য নিচের ডায়াগ্রামটা দেখা যাক।

minibatch

এই পর্ব এই পর্যন্তই। পরবর্তী পর্বে গ্রেডিয়েন্ট ডিসেন্টের নরমাল রিপ্রেজেন্টেশন দেখানো হবে।