torch_Python_regression.qmd

---
title: "Introduction à Pytorch"
subtitle: "Traduction de la version `{torch}` en `pytorch`"
lang: fr
execute: 
  freeze: auto
output: 
  html_document:
    toc: true
    toc_float: true
---

Cette page constitue une traduction en Python avec pytorch de la [page équivalente](https://stateofther.github.io/finistR2022/autodiff.html) produite avec `{torch}` lors de FinistR 2022. 

## Installation 

Une façon (parmi d'autres) d'avoir une installation fonctionnelle de torch consiste à l'installer via conda. La [page officielle](https://pytorch.org/get-started/locally/) est très bien documentée et fournit toutes les instructions nécessaires. La solution adoptée ici consiste à créer un environnement conda (nommé torch) pour y installer torch (en version CPU). 

```{bash}
#| eval: false
conda create -n torch
conda install pytorch torchvision torchaudio cpuonly -c pytorch
conda install pandas matplotlib scikit-learn jupyter
```

Il suffit alors d'activer l'environnement torch pour produire le html à partir du qmd

```{bash}
#| eval: false
conda activate torch
quarto render my_document.qmd --to html
```

## Exploration de `{torch}` pour la différentiation automatique

```{python}
import torch
import torch.distributions as dist
import torch.optim as optim
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LinearRegression
```

## Principe du calcul de gradient

`{torch}` fonctionne avec ses propres types numériques, qu’il faut créer avec la fonction `torch.tensor()` et ses propres fonctions `torch.*()`. Considérons un exemple très simple: $x \mapsto x^2$

```{python}
x = torch.tensor(3)
y = torch.square(x)
```

```{python}
y
```

On va pouvoir calculer $\frac{dy}{dx}$ en définissant `x` avec l'argument `require_grad = True`. Cet argument va spécifier que 'x' est entrainable et va démarrer l'enregistrement par autograd des opérations sur ce tenseur.

Autograd est un module de `torch` qui permet de collecter les gradients. Il le fait en enregistrant des données (tenseurs) et toutes les opérations exécutées dans un graphe acyclique dirigé dont les feuilles sont les tenseurs d'entrée et les racines les tenseurs de sorties. Ces opérations sont stockées comme des fonctions et au moment du calcul des gradients, sont appliquées depuis le noeud de sortie en 'backpropagation' le long du réseau.

**Attention**, torch ne peut stocker un gradient que pour des valeurs numériques (`float`), pas pour des entiers. 

```{python}
x = torch.tensor(2.0, requires_grad = True)
x
```

On remarque que `x` possède désormais un champ `grad` (même si ce dernier n'est pas encore défini).

```{python}
x.grad
```

Lorsqu'on calcule $y = x^2$, ce dernier va également hériter d'un nouveau champ `$grad_fn`:

```{python}
y = torch.log(torch.square(x))
y
y.grad_fn
```

qui indique comment calculer le gradient en utilisant la dérivée des fonctions composées:

$$
(g\circ f)'(x) = f'(x) \times g'(f(x))
$$

et les fonctions

$$
\frac{dx^2}{dx} = 2x \quad \frac{d \log(x)}{dx} = \frac{1}{x}
$$

Le calcul effectif du gradient est déclenché lors de l'appel à la méthode `.backward()` de `y` et est stocké dans le champ `.grad` de `x`.

```{python}
x.grad ## gradient non défini
y.backward() 
x.grad ## gradient défini = 1
```

On a bien:

$$
\frac{dy}{dx} = \underbrace{\frac{dy}{dz}}_{\log}(z) \times \underbrace{\frac{dz}{dx}}_{\text{power}}(x) = \frac{1}{4} \times 2*2 = 1
$$ 

Intuitivement au moment du calcul de `y`, `torch` construit un graphe computationnel qui lui permet d'évaluer **numériquement** $y$ et qui va **également** servir pour calculer $\frac{dy}{dz}$ au moment de l'appel à la fonction `.backward()` issue du module autograd.

Essayons de reproduire le calcul dans notre exemple. Le calcul **forward** donne

$$
x = 2 \xrightarrow{x \mapsto x^2} z = 4 \mapsto \xrightarrow{x \mapsto \log(x)} y = \log(4)
$$

Pour le calcul **backward**, il faut donc construire le graphe formel suivant. La première étape du graphe est accessible via `$grad_fn`

```{python}
y.grad_fn
```

et les fonctions suivantes via `$next_functions`

```{python}
y.grad_fn.next_functions
```

Dans notre exemple, on a donc:

$$
\frac{dy}{dy} = 1 \xrightarrow{x \mapsto \text{logBackward}(x)} \frac{dy}{dz} = \frac{dy}{dy} \times \text{logBackward}(z) \xrightarrow{x \mapsto \text{powerBackward}(x)} \frac{dy}{dx} = \frac{dy}{dz} \times \text{logBackward}(x)
$$

Dans cet exemple:

-   $\text{logBackward}(x) = \frac{1}{x}$
-   $\text{powBackward}(x) = 2x$

Et la propagation des dérivées donne donc

$$
\frac{dy}{dy} = 1 \to \frac{dy}{dz} = 1 \times \frac{1}{4} = \frac{1}{4} \to \frac{dy}{dx} = \frac{1}{4} \times 4 = 1
$$

Ce graphe est illustré ci-dessous pour la fonction $(x_1, x_2) \mapsto z = sin(x_2) log(x_1 x_2)$

![](https://pytorch.org/assets/images/augmented_computational_graph.png)

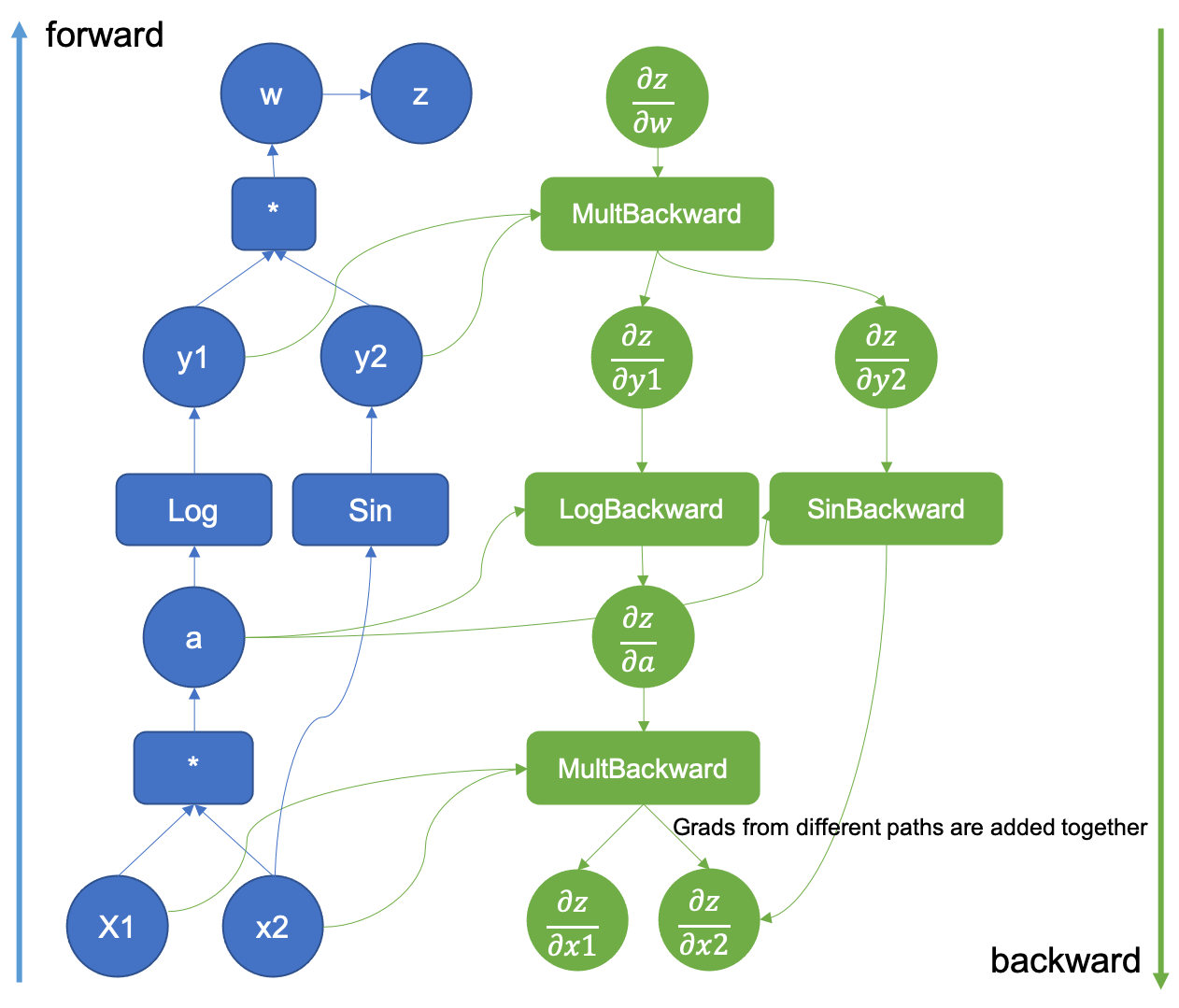
Pour (beaucoup) plus de détails sur le graphe computationnel, on peut consulter la [documentation officielle de PyTorch](https://pytorch.org/blog/how-computational-graphs-are-executed-in-pytorch/).

Il faut juste noter que dans `torch`, le graphe computationnel est construit de **façon dynamique**, au moment du calcul de `y`.

## Régression logistique avec `torch`

On va adopter un simple modèle de régression logistique:

$$
Y_i \sim \mathcal{B}(\sigma(\theta^T x_i)) \quad \text{avec} \quad \sigma(x) = \frac{1}{1 + e^{x}}
$$

Le but est d'estimer $\theta$ et éventuellement les erreurs associées. On commence par générer des données.

```{python}
# Générer les paramètres
torch.manual_seed(45)
n = 100
p = 3
# Générer la matrice X
X = torch.randn(n, p)
# Générer le vecteur theta
theta = torch.randn(3)
# Calculer les probabilités
probs = 1 / (1 + torch.exp(torch.mv(X, theta)))
# Générer les observations Y en utilisant une distribution Bernoulli
bernoulli_dist = dist.Bernoulli(probs=probs)
Y = bernoulli_dist.sample()
```

`torch` fonctionne avec ses propres types numériques, qu'il faut créer avec la fonction `torch.tensor()`. C'est ce qu'on a fait avec les fonctions `torch.randn()` et `bernoulli_dist.sample()` mais on pourrait forcer la conversion avec `torch.tensor()`. 

```{python}
x = X.clone()
y = Y.clone()
```

On écrit ensuite la fonction de vraisemblance

$$
\mathcal{L}(\mathbf{X}, \mathbf{y}; \theta) = \sum_{i=1}^n y_i (\theta^Tx_i) - \sum_{i=1}^n log(1 + e^{\theta^T x_i})
$$

```{python}
def logistic_loss(theta, x, y):
    odds = torch.mv(x, theta)
    log_lik = torch.dot(y, odds) - torch.sum(torch.log(1 + torch.exp(odds)))
    return -log_lik
```

avant de vérifier qu'elle fonctionne:

```{python}
logistic_loss(theta = theta, x = x, y = y)
```

On veut ensuite définir une fonction objective à maximiser (qui ne dépend que de `theta`):

```{python}
def eval_loss(theta, verbose=True):
    loss = logistic_loss(theta, x, y)
    if verbose:
        print("Theta:", theta, ": Loss:", float(loss))
    return loss
```

et vérifier qu'elle fonctionne

```{python}
eval_loss(theta, verbose = True)
```

avant de procéder à l'optimisation à proprement parler. Pour cette dernière, on commence par définir notre paramètre sous forme d'un tenseur qui va être mis à jour

```{python}
theta_current = torch.zeros(len(theta), requires_grad=True)
```

et d'un optimiseur:

```{python}
optimizer = optim.Rprop([theta_current])
```

On considère ici l'optimiseur Rprop (resilient backpropagation) qui ne prend pas en compte l'amplitude du gradient mais uniquement le signe de ses coordonnées (voir [ici pour une introduction pédagogique à Rprop](https://florian.github.io/rprop/)). 

Intuitivement, l'optimiseur a juste besoin de la valeur de $\theta$ et de son gradient pour le mettre à jour. Mais à ce stade on ne connaît pas encore le gradient $\nabla_\theta \mathcal{L}(\mathbf{X}, \mathbf{y}; \theta)$

```{python}
theta_current.grad
```

et il faut donc le calculer:

```{python}
loss = eval_loss(theta_current, verbose = False)
loss.backward()
```

On peut vérifier que le gradient est stocké dans `theta`

```{python}
theta_current.grad
```

et effectuer la mise à jour avec une étape d'optimisation

```{python}
optimizer.step()
```

On peut vérifier que le paramètre courant a été mis à jour.

```{python}
theta_current
```

Il ne reste plus qu'à recommencer pour un nombre d'itérations donné. **Attention,** il faut réinitialiser le gradient avant de le mettre à jour, le comportement par défaut de mise à jour étant l'*accumulation* plutôt que le *remplacement*.

```{python}
num_iterations = 100
loss_vector = []

for i in range(num_iterations):
    optimizer.zero_grad()
    loss = eval_loss(theta_current, verbose=False)
    loss.backward()
    optimizer.step()
    loss_vector.append(loss.item())
```

On vérifie que la perte diminue au cours du temps.

```{python}
plt.plot(range(1, num_iterations + 1), loss_vector)
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Loss vs. Iterations')
plt.show()
```

On constate que notre optimiseur aboutit à peu près au même résultat que `glm()`

```{python}
# Ajustement du modèle GLM
model = LogisticRegression(fit_intercept=False, penalty = None)
model.fit(X, Y)
sklearn_coeffs = model.coef_.tolist()[0]

# Comparer les valeurs obtenues avec torch et glm
df = pd.DataFrame({
    'torch': theta_current.detach().numpy().tolist(),
    'sklearn': sklearn_coeffs
})
print(df)
```

**Attention** la mécanique présentée ci-dessus avec `.step()` ne fonctionne pas pour certaines routines d'optimisation (BFGS, gradient conjugué) qui nécessite de calculer plusieurs fois la fonction objective. Dans ce cas, il faut définir une *closure*, qui renvoie la fonction objective, et la passer en argument à `.step()`.

```{python}
%%time
# Remise à zéro du paramètre courant
theta_current = torch.zeros(len(theta), requires_grad=True)
optimizer = optim.Rprop([theta_current], lr=0.01)

# Définition de la closure
def calc_loss():
    optimizer.zero_grad()
    loss = eval_loss(theta_current, verbose=False)
    loss.backward()
    return loss

# Optimisation avec la closure
num_iterations = 100
loss_vector = []

for i in range(num_iterations):
    loss = optimizer.step(calc_loss).item()
    loss_vector.append(loss)
```

On peut vérifier qu'on obtient des résultats identiques dans les deux cas d'utilisation:

```{python}
theta_current
```

```{python}
plt.plot(range(1, num_iterations + 1), loss_vector)
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Loss vs. Iterations')
plt.show()
```

## Exemple de régression multivariée

On considère un exemple de régression multiple, réalisé à partir du blog [torch for optimization](https://blogs.rstudio.com/ai/posts/2021-04-22-torch-for-optimization/), où l'on cherche à estimer les paramètres de moyenne ainsi que la variance par maximisation de la vraisemblance.

On génère les données

```{python}
# Définir la graine aléatoire pour la reproductibilité
torch.manual_seed(45)
# Générer la matrice X
n = 100
X = torch.cat((torch.ones(n, 1), torch.randn(n, 10)), dim=1)
# Générer le vecteur Beta.true
Beta_true = torch.randn(11)
# Générer la variable dépendante Y
Y = torch.matmul(X, Beta_true) + torch.randn(n)
```

La fonction de perte à optimiser (ici la log-vraisemblance) va dépendre d'inputs définis comme des "tenseurs torch":

```{python}
## Declare the parameter for the loss function
## 11 parameters for Beta, 1 for sigma
Theta = torch.ones(12, requires_grad = True)
```

Quelques remarques :

- le paramètre $\theta$ à optimiser est ici défini comme un tenseur, i.e. un objet qui va notamment stocker la valeur courante de $\theta$. Avec l'option `requires_grad=True` la valeur courante du gradient de la dernière fonction appelée dépendant de $\theta$ va aussi être stockée.

- la matrice $X$ est aussi définie comme un tenseur, mais l'option "requires_grad=TRUE" n'a pas été spécifiée, le gradient ne sera donc pas stocké pour cet objet. Cette distinction est explicitée lorsque l'on affiche les deux objets:

```{python}
Theta[:3]
X[:3, :3]
```

La fonction de perte est ici la log-vraisemblance, elle-même définie à partir d'opérateurs torch élémentaires :

```{python}
def LogLik():
    n = X.shape[0]  
    # Last term of Theta is the std
    sigma = Theta[11]
    log_sigma = torch.log(sigma)
    squared_residuals = torch.norm(Y - torch.matmul(X, Theta[:11])) ** 2
    term1 = n * log_sigma
    term2 = squared_residuals / (2 * (sigma ** 2))
    return term1 + term2
```

La fonction LogLik peut être appliquée comme une fonction R qui prendra directement en argument les valeurs courantes de X.tensor et $\theta$, et produira en sortie un tenseur

```{python}
LogLik()
```

Outre la valeur courante de la fonction, ce tenseur contient la "recette" du graphe computationnel utilisé dans calcul backward du gradient de la fonction LogLik par rapport à $\theta$. On peut ainsi afficher la dernière opération de ce graphe

```{python}
toto = LogLik()
toto.grad_fn
```

correspondant à l'addition (AddBackward) des deux termes $$  n\times \log(\theta[11]) \quad \text{et} \quad ||Y-X\theta[0:10]||^2/(2*\theta[11]^2)$$ dans le calcul de la perte. On peut afficher les opérations suivantes dans le graphe comme suit:

```{python}
toto.grad_fn.next_functions
```

L'étape suivante consiste à choisir la méthode d'optimisation à appliquer. L'intérêt d'utiliser le package `{torch}` est d'avoir accès à une large gamme de méthodes d'optimisation, on considère ici la méthode rprop qui réalise une descente de gradient à pas adaptatif et spécifique à chaque coordonnée:

```{python}
## Specify the optimization parameters
lr = 0.01
optimizer = optim.Rprop([Theta],lr)
```

On décrit maintenant un pas de calcul du gradient, contenant les étapes suivantes : - réinitialisation du gradient de $\theta$,\
- évaluation de la fonction de perte (avec la valeur courante de $\theta$),\
- calcul backward du gradient. On inclut tout cela dans une fonction:

```{python}
## Optimization step description
def calc_loss():
    optimizer.zero_grad()
    value = LogLik()
    value.backward()
    return value
```

Commençons par regarder ce que fait concrètement cette fonction. L'état courant du paramètre est le suivant:

```{python}
Theta
Theta.grad
```

On applique une première fois la fonction, et on obtient la mise à jour suivante :

```{python}
calc_loss()
Theta
Theta.grad
```

Comme on le voit la valeur courante du paramètre n'a pas changée, en revanche `Theta.grad` contient maintenant le gradient de la fonction de perte calculé en $\theta$. Dans le cas où la méthode d'optimisation considérée n'a besoin que de la valeur courante du gradient et du paramètre, on peut directement faire la mise à jour de $\theta$ :

```{python}
optimizer.step()
Theta
Theta.grad
```

Il n'y a plus qu'à itérer !

```{python}
%%time
## Run the optimization
num_iterations = 100
loss_vector = torch.empty(num_iterations)

for i in range(num_iterations):
    loss_vector[i] = calc_loss().item()
    optimizer.step()
```

On vérifie que l'optimisation s'est bien passée (ie que l'on a minimisé la fonction de perte)

```{python}
## How does the loss function behave ?
plt.plot(range(1, num_iterations + 1), loss_vector)
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.title('Loss vs. Iterations')
plt.show()

## Are the gradients at 0 ?
Theta.grad
```

et que le résultat est comparable à la solution classique obtenue par OLS :

```{python}
# Ajuster un modèle de régression linéaire avec scikit-learn
regressor = LinearRegression(fit_intercept=False)
regressor.fit(X, Y)

# Obtenir les coefficients du modèle
beta_hat = regressor.coef_

# Afficher les coefficients et tracer une ligne y = x
print("Coefficients du modèle de régression linéaire :\n", beta_hat)
print("Coefficients de Theta :\n", Theta[:11].detach().numpy().tolist())

# Tracer la ligne y = x pour la comparaison
plt.scatter(beta_hat, Theta[:11].detach().numpy().tolist())
plt.plot([beta_hat.min(), beta_hat.max()], [beta_hat.min(), beta_hat.max()], color='red', linestyle='--')
plt.xlabel('Coefficients du modèle de régression linéaire')
plt.ylabel('Coefficients de Theta')
plt.title('Comparaison des coefficients')
plt.show()

# Calculer la variance des résidus
residuals = Y - torch.matmul(X, torch.tensor(beta_hat).t())
sigma_squared_lm = np.var(residuals.detach().numpy())
sigma_squared_theta = Theta[11]

print("Variance du modèle de régression linéaire :", sigma_squared_lm)
print("Variance de Theta[12] :", sigma_squared_theta.item())
```