building-boxes

< Previous 　　　　　　　　　　　　　　　　 Next >

1739. Building Boxes (Hard)

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

• You can place the boxes anywhere on the floor.
• If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return the minimum possible number of boxes touching the floor.

 

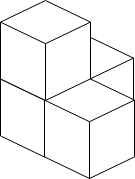
Example 1:

Input: n = 3
Output: 3
Explanation: The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

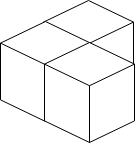
Example 2:

Input: n = 4
Output: 3
Explanation: The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

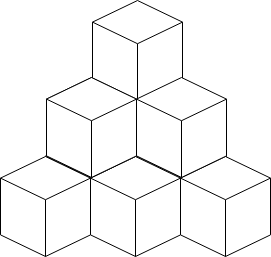
Example 3:

Input: n = 10
Output: 6
Explanation: The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.

 

Constraints:

• 1 <= n <= 109

Related Topics

[Greedy] [Math] [Binary Search]

Hints

Hint 1

Suppose We can put m boxes on the floor, within all the ways to put the boxes, what’s the maximum number of boxes we can put in?

Hint 2

The first box should always start in the corner