maximum-binary-tree-ii

< Previous 　　　　　　　　　　　　　　　　 Next >

998. Maximum Binary Tree II (Medium)

A maximum tree is a tree where every node has a value greater than any other value in its subtree.

You are given the root of a maximum binary tree and an integer val.

Just as in the previous problem, the given tree was constructed from a list a (root = Construct(a)) recursively with the following Construct(a) routine:

• If a is empty, return null.
• Otherwise, let a[i] be the largest element of a. Create a root node with the value a[i].
• The left child of root will be Construct([a[0], a[1], ..., a[i - 1]]).
• The right child of root will be Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]).
• Return root.

Note that we were not given a directly, only a root node root = Construct(a).

Suppose b is a copy of a with the value val appended to it. It is guaranteed that b has unique values.

Return Construct(b).

 

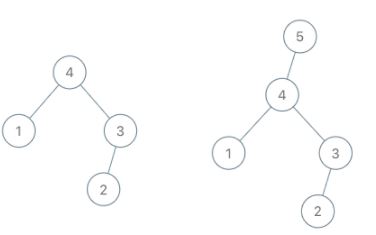
Example 1:

Input: root = [4,1,3,null,null,2], val = 5
Output: [5,4,null,1,3,null,null,2]
Explanation: a = [1,4,2,3], b = [1,4,2,3,5]

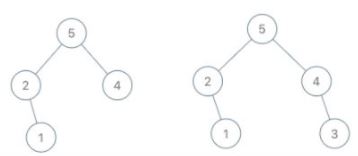
Example 2:

Input: root = [5,2,4,null,1], val = 3
Output: [5,2,4,null,1,null,3]
Explanation: a = [2,1,5,4], b = [2,1,5,4,3]

Example 3:

Input: root = [5,2,3,null,1], val = 4
Output: [5,2,4,null,1,3]
Explanation: a = [2,1,5,3], b = [2,1,5,3,4]

 

Constraints:

• The number of nodes in the tree is in the range [1, 100].
• 1 <= Node.val <= 100
• All the values of the tree are unique.
• 1 <= val <= 100

Related Topics

[Tree] [Binary Tree]

Similar Questions

1. Maximum Binary Tree (Medium)