maximum-sum-bst-in-binary-tree

< Previous 　　　　　　　　　　　　　　　　 Next >

1373. Maximum Sum BST in Binary Tree (Hard)

Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than the node's key.
• Both the left and right subtrees must also be binary search trees.

 

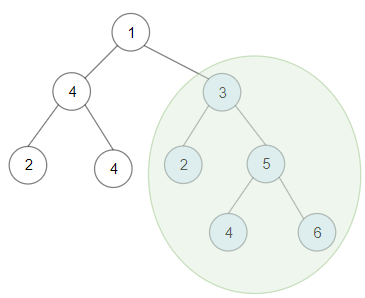
Example 1:

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

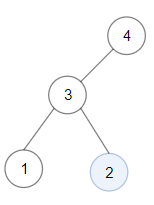
Example 2:

Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

Example 3:

Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.

 

Constraints:

• The number of nodes in the tree is in the range [1, 4 * 104].
• -4 * 104 <= Node.val <= 4 * 104

Related Topics

[Dynamic Programming] [Tree] [Depth-First Search] [Binary Search Tree] [Binary Tree]

Hints

Hint 1

Create a datastructure with 4 parameters: (sum, isBST, maxLeft, minLeft).

Hint 2

In each node compute theses parameters, following the conditions of a Binary Search Tree.