Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.
It is guaranteed that the answer will in the range of 32-bit signed integer.
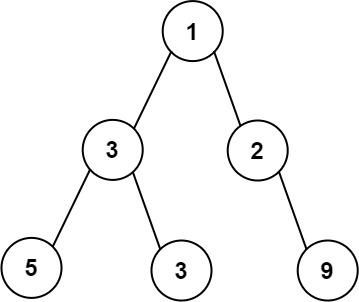
Example 1:
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).
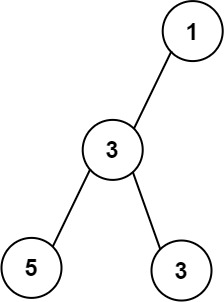
Example 2:
Input: root = [1,3,null,5,3] Output: 2 Explanation: The maximum width existing in the third level with the length 2 (5,3).
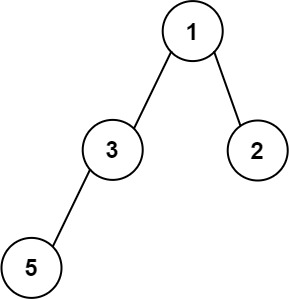
Example 3:
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width existing in the second level with the length 2 (3,2).
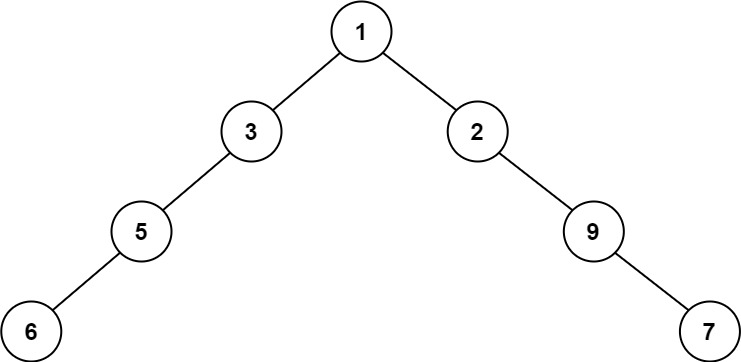
Example 4:
Input: root = [1,3,2,5,null,null,9,6,null,null,7] Output: 8 Explanation: The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
[Tree] [Depth-First Search] [Breadth-First Search] [Binary Tree]