You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
For class emcee.moves.GaussianMove(cov, mode='vector', factor=None), the emcee docs (and the comments in the source code) all say the parameter factor (Optional[float]) is invalid for the "vector" mode. However, I do not find factor option is forbidden in actual calculation of proposal samples when mode="vector" in the following code.
Also, I don't quite understand mathematically why factor (Optional[float])` is invalid for the "vector" mode.
As far as I understand, factor (Optional[float]) makes the Gaussian with flexible scale (i.e., add a factor to the fixed input scale parameter), which somewhat introduce more randomness to benefit the proposal.
Then the proposal distribution turn out to be
Here, x is the proposal sample, G represent Gaussian distribution, cov and factor are the input parameters, f is the proposal factor value in actual calculation, which follows LogUniform(-self.log_factor, self.log_factor) in this line.
From my understanding, the proposal distribution keeps a symmetric distribution, which means we do not need to introduce additional factor to account for difference in proposal distribution q(x|x') and q(x'|x) when calculating the acceptance rate in MCMC, i.e., the same as a regular Gaussian proposal.
And it's nothing related to mode if I understand correctly.
Also, another question comes to me when thinking of the mode. If one provides the full, square covariance matrix and choose "random", or "sequential" mode, that means, sampler selects one dimension in each iteration, proposal distribution becomes marginalized Gaussian in this situation. Only the variance element will affect the proposal but the covariance (non-diagonal elements) won't be considered. That's probably a loss of information. Maybe "random", or "sequential" mode should be disabled in this case?
I may make some mistakes when thinking of all these. Please correct me if there're some problems.
Thanks!
The text was updated successfully, but these errors were encountered:
For class
emcee.moves.GaussianMove(cov, mode='vector', factor=None), the emcee docs (and the comments in the source code) all say the parameterfactor (Optional[float])is invalid for the "vector" mode. However, I do not find factor option is forbidden in actual calculation of proposal samples when mode="vector" in the following code.Also, I don't quite understand mathematically why factor (Optional[float])` is invalid for the "vector" mode.
As far as I understand,
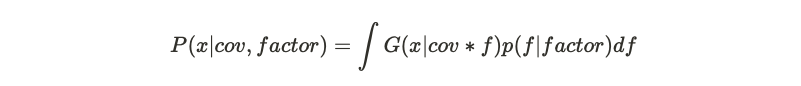
factor (Optional[float])makes the Gaussian with flexible scale (i.e., add a factor to the fixed input scale parameter), which somewhat introduce more randomness to benefit the proposal.Then the proposal distribution turn out to be
Here, x is the proposal sample, G represent Gaussian distribution,
covandfactorare the input parameters, f is the proposal factor value in actual calculation, which followsLogUniform(-self.log_factor, self.log_factor)in this line.From my understanding, the proposal distribution keeps a symmetric distribution, which means we do not need to introduce additional factor to account for difference in proposal distribution
q(x|x')andq(x'|x)when calculating the acceptance rate in MCMC, i.e., the same as a regular Gaussian proposal.And it's nothing related to mode if I understand correctly.
Also, another question comes to me when thinking of the mode. If one provides the full, square covariance matrix and choose
"random", or"sequential"mode, that means, sampler selects one dimension in each iteration, proposal distribution becomes marginalized Gaussian in this situation. Only the variance element will affect the proposal but the covariance (non-diagonal elements) won't be considered. That's probably a loss of information. Maybe"random", or"sequential"mode should be disabled in this case?I may make some mistakes when thinking of all these. Please correct me if there're some problems.
Thanks!
The text was updated successfully, but these errors were encountered: