forked from shunliz/Machine-Learning
-
Notifications
You must be signed in to change notification settings - Fork 0
/
Copy pathsmo.md
267 lines (134 loc) · 10.9 KB
/
smo.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
# [SMO算法原理](http://www.cnblogs.com/pinard/p/6111471.html)
---
# 1. 回顾SVM优化目标函数
我们首先回顾下我们的优化目标函数:
$$
min(\alpha)\;\; \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jK(x_i,x_j) - \sum\limits_{i=1}^{m}\alpha_i
$$
$$
s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0
$$
$$
0 \leq \alpha_i \leq C
$$
我们的解要满足的KKT条件的对偶互补条件为:$$\alpha_{i}^{*}(y_i(w^{*} \bullet \phi(x_i) + b^{*}) - 1) = 0$$
根据这个KKT条件的对偶互补条件,我们有:
$$
\alpha_{i}^{*} = 0 \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b) \geq 1
$$
$$
0 \leq \alpha_{i}^{*} \leq C \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b) = 1
$$
$$
\alpha_{i}^{*}= C \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b) \leq 1
$$
由于$$w^{*} = \sum\limits_{j=1}^{m}\alpha_j^{*}y_j\phi(x_j)$$,我们令$$g(x) = w^{*} \bullet \phi(x) + b =\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*}$$,则有:
$$
\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i) \geq 1
$$
$$
0 \leq \alpha_{i}^{*} \leq C \Rightarrow y_ig(x_i) = 1
$$
$$
\alpha_{i}^{*}= C \Rightarrow y_ig(x_i) \leq 1
$$
# 2. SMO算法的基本思想
上面这个优化式子比较复杂,里面有m个变量组成的向量$$\alpha$$需要在目标函数极小化的时候求出。直接优化时很难的。SMO算法则采用了一种启发式的方法。它每次只优化两个变量,将其他的变量都视为常数。由于$$\sum\limits_{i=1}^{m}\alpha_iy_i = 0$$.假如将$$\alpha_3, \alpha_4, ..., \alpha_m$$ 固定,那么$$\alpha_1, \alpha_2$$之间的关系也确定了。这样SMO算法将一个复杂的优化算法转化为一个比较简单的两变量优化问题。
为了后面表示方便,我们定义$$K_{ij} = \phi(x_i) \bullet \phi(x_j)$$
由于$$\alpha_3, \alpha_4, ..., \alpha_m$$都成了常量,所有的常量我们都从目标函数去除,这样我们上一节的目标优化函数变成下式:
$$
min(\alpha_1, \alpha_1)\;\; \frac{1}{2}K_{11}\alpha_1^2 + \frac{1}{2}K_{22}\alpha_2^2 +y_1y_2K_{12}\alpha_1 \alpha_2 -(\alpha_1 + \alpha_2) +y_1\alpha_1\sum\limits_{i=3}^{m}y_i\alpha_iK_{i1} + y_2\alpha_2\sum\limits_{i=3}^{m}y_i\alpha_iK_{i2}
$$
$$
s.t. \;\;\alpha_1y_1 + \alpha_2y_2 = -\sum\limits_{i=3}^{m}y_i\alpha_i = \varsigma
$$
$$
0 \leq \alpha_i \leq C \;\; i =1,2
$$
# 3. SMO算法目标函数的优化
为了求解上面含有这两个变量的目标优化问题,我们首先分析约束条件,所有的$$\alpha_1, \alpha_2$$都要满足约束条件,然后在约束条件下求最小。
根据上面的约束条件$$\alpha_1y_1 + \alpha_2y_2 = \varsigma\;\;0 \leq \alpha_i \leq C \;\; i =1,2$$,又由于$$y_1,y_2$$均只能取值1或者-1, 这样$$\alpha_1, \alpha_2$$在\[0,C\]和\[0,C\]形成的盒子里面,并且两者的关系直线的斜率只能为1或者-1,也就是说$$\alpha_1, \alpha_2$$的关系直线平行于\[0,C\]和\[0,C\]形成的盒子的对角线,如下图所示:
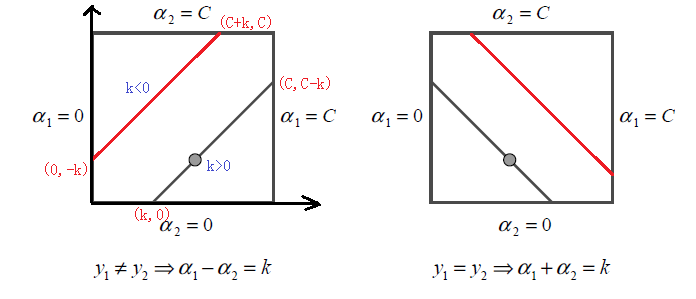
由于$$\alpha_1, \alpha_2$$的关系被限制在盒子里的一条线段上,所以两变量的优化问题实际上仅仅是一个变量的优化问题。不妨我们假设最终是$$\alpha_2$$的优化问题。由于我们采用的是启发式的迭代法,假设我们上一轮迭代得到的解是$$\alpha_1^{old}, \alpha_2^{old}$$,假设沿着约束方向$$\alpha_2$$未经剪辑的解是$$\alpha_2^{new,unc}$$.本轮迭代完成后的解为$$\alpha_1^{new}, \alpha_2^{new}$$
由于$$\alpha_2^{new}$$必须满足上图中的线段约束。假设L和H分别是上图中$$\alpha_2^{new}$$所在的线段的边界。那么很显然我们有:$$L \leq \alpha_2^{new} \leq H$$
而对于L和H,我们也有限制条件如果是上面左图中的情况,则
$$
L = max(0, \alpha_2^{old}-\alpha_1^{old}) \;\;\;H = min(C, C+\alpha_2^{old}-\alpha_1^{old})
$$
如果是上面右图中的情况,我们有:
$$
L = max(0, \alpha_2^{old}+\alpha_1^{old}-C) \;\;\; H = min(C, \alpha_2^{old}+\alpha_1^{old})
$$
也就是说,假如我们通过求导得到的$$\alpha_2^{new,unc}$$,则最终的$$\alpha_2^{new}$$应该为:
$$\alpha_2^{new}= \begin{cases} H& {L \leq \alpha_2^{new,unc} > H}\\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\\ L& {\alpha_2^{new,unc} < L} \end{cases}$$
那么如何求出$$\alpha_2^{new,unc}$$呢?很简单,我们只需要将目标函数对$$\alpha_2$$求偏导数即可。
首先我们整理下我们的目标函数。
为了简化叙述,我们令$$E_i = g(x_i)-y_i = \sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x_i, x_j)+ b - y_i$$,
其中g\(x\)就是我们在第一节里面的提到的$$g(x) = w^{*} \bullet \phi(x) + b =\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*}$$
我们令$$v_i = \sum\limits_{i=3}^{m}y_j\alpha_jK(x_i,x_j) = g(x_i) - \sum\limits_{i=1}^{2}y_j\alpha_jK(x_i,x_j) -b$$
这样我们的优化目标函数进一步简化为:$$W(\alpha_1,\alpha_2) = \frac{1}{2}K_{11}\alpha_1^2 + \frac{1}{2}K_{22}\alpha_2^2 +y_1y_2K_{12}\alpha_1 \alpha_2 -(\alpha_1 + \alpha_2) +y_1\alpha_1v_1 + y_2\alpha_2v_2$$
由于$$\alpha_1y_1 + \alpha_2y_2 = \varsigma$$,并且$$y_i^2 = 1$$,可以得到$$\alpha_1$$用$$\alpha_2$$表达的式子为:$$\alpha_1 = y_1(\varsigma - \alpha_2y_2)$$
将上式带入我们的目标优化函数,就可以消除$$\alpha_1$$,得到仅仅包含$$\alpha_2$$的式子。$$W(\alpha_2) = \frac{1}{2}K_{11}(\varsigma - \alpha_2y_2)^2 + \frac{1}{2}K_{22}\alpha_2^2 +y_2K_{12}(\varsigma - \alpha_2y_2) \alpha_2 -(\alpha_1 + \alpha_2) +(\varsigma - \alpha_2y_2)v_1 + y_2\alpha_2v_2$$
忙了半天,我们终于可以开始求$$\alpha_2^{new,unc}$$了,现在我们开始通过求偏导数来得到$$\alpha_2^{new,unc}$$。
$$\frac{\partial W}{\partial \alpha2} = K{11}\alpha2 + K{22}\alpha2 -2K{12}\alpha2 - K{11}\varsigma y2 + K{12}\varsigma y_2 +y_1y_2 -1 -v_1y_2 +y_2v_2 = 0$$
整理上式有:$$(
K{11} +K{22}-2K{12})\alpha_2 = y_2(y_2-y_1 + \varsigma K{11} - \varsigma K_{12} + v_1 - v_2) $$
$$= y_2(y_2-y_1 + \varsigma K_{11} - \varsigma K_{12} + (g(x_1) - \sum\limits_{j=1}^{2}y_j\alpha_jK_{1j} -b ) -(g(x_2) - \sum\limits_{j=1}^{2}y_j\alpha_jK_{2j} -b))$$
将$$\varsigma = \alpha_1y_1 + \alpha_2y_2$$带入上式,我们有:
$$(K_{11} +K_{22}-2K_{12})\alpha_2^{new,unc} = y_2((K_{11} +K_{22}-2K_{12})\alpha_2^{old}y_2 +y_2-y_1 +g(x_1) - g(x_2))$$
$$\;\;\;\; = (K_{11} +K_{22}-2K_{12}) \alpha_2^{old} + y2(E_1-E_2)$$
我们终于得到了$$\alpha_2^{new,unc}$$的表达式:$$\alpha_2^{new,unc} = \alpha_2^{old} + \frac{y2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
利用上面讲到的$$\alpha_2^{new,unc}$$和$$\alpha_2^{new}$$的关系式,我们就可以得到我们新的$$\alpha_2^{new}$$了。利用$$\alpha_2^{new}$$和$$\alpha_1^{new}$$的线性关系,我们也可以得到新的$$\alpha_1^{new}$$。
# 4. SMO算法两个变量的选择
SMO算法需要选择合适的两个变量做迭代,其余的变量做常量来进行优化,那么怎么选择这两个变量呢?
## 4.1 第一个变量的选择
SMO算法称选择第一个变量为外层循环,这个变量需要选择在训练集中违反KKT条件最严重的样本点。对于每个样本点,要满足的KKT条件我们在第一节已经讲到了:
$$
\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i) \geq 1
$$
$$
0 \leq \alpha_{i}^{*} \leq C \Rightarrow y_ig(x_i) =1
$$
$$
\alpha_{i}^{*}= C \Rightarrow y_ig(x_i) \leq 1
$$
一般来说,我们首先选择违反$$0 \leq \alpha_{i}^{*} \leq C \Rightarrow y_ig(x_i) =1$$这个条件的点。如果这些支持向量都满足KKT条件,再选择违反$$\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i) \geq 1 $$和$$\alpha_{i}^{*}= C \Rightarrow y_ig(x_i) \leq 1$$的点。
## 4.2 第二个变量的选择
SMO算法称选择第二个变量为内层循环,假设我们在外层循环已经找到了$$\alpha_1$$, 第二个变量$$\alpha_2$$的选择标准是让\|E1-E2\|有足够大的变化。由于$$\alpha_1$$定了的时候,$$E_1$$也确定了,所以要想\|E1-E2\|最大,只需要在$$E_1$$为正时,选择最小的$$E_i$$作为$$E_2$$, 在$$E_1$$为负时,选择最大的$$E_i$$作为$$E_2$$,可以将所有的$$E_i$$保存下来加快迭代。
如果内存循环找到的点不能让目标函数有足够的下降, 可以采用遍历支持向量点来做$$\alpha_2$$,直到目标函数有足够的下降, 如果所有的支持向量做$$\alpha_2$$都不能让目标函数有足够的下降,可以跳出循环,重新选择$$\alpha_1$$
## 4.3 计算阈值b和差值E\_i
在每次完成两个变量的优化之后,需要重新计算阈值b。当$$0 \leq \alpha_{1}^{new} \leq C$$时,我们有$$y_1 - \sum\limits_{i=1}^{m}\alpha_iy_iK_{i1} -b_1 = 0$$
于是新的$$b_1^{new}$$为:$$b_1^{new} = y_1 - \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1} - \alpha_{1}^{new}y_1K_{11} - \alpha_{2}^{new}y_2K_{21}$$
计算出$$E_1$$为:$$E_1 = g(x_1) - y_1 = \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1} + \alpha_{1}^{old}y_1K_{11} + \alpha_{2}^{old}y_2K_{21} + b^{old} -y_1$$
可以看到上两式都有$$y_1 - \sum\limits_{i=3}^{m}\alpha_iy_iK_{i1}$$,因此可以将$$b_1^{new}$$用$$E_1$$表示为:$$b_1^{new} = -E_1 -y_1K_{11}(\alpha_{1}^{new} - \alpha_{1}^{old}) -y_2K_{21}(\alpha_{2}^{new} - \alpha_{2}^{old}) + b^{old}$$
同样的,如果$$0 \leq \alpha_{2}^{new} \leq C$$, 那么有:$$b_2^{new} = -E_2 -y_1K_{12}(\alpha_{1}^{new} - \alpha_{1}^{old}) -y_2K_{22}(\alpha_{2}^{new} - \alpha_{2}^{old}) + b^{old}$$
最终的$$b^{new}$$为:$$b^{new} = \frac{b_1^{new} + b_2^{new}}{2}$$
得到了$$b^{new}$$我们需要更新$$E_i:E_i = \sum\limits_{S}y_j\alpha_jK(x_i,x_j) + b^{new} -y_i$$
其中,S是所有支持向量$$x_j$$的集合。
好了,SMO算法基本讲完了,我们来归纳下SMO算法。
# 5. SMO算法总结
输入是m个样本$${(x_1,y_1), (x_2,y_2), ..., (x_m,y_m),}$$,其中x为n维特征向量。y为二元输出,值为1,或者-1.精度e。
输出是近似解\alpha
1\)取初值$$\alpha^{0} = 0, k =0$$
2\)按照4.1节的方法选择$$\alpha_1^k$$,接着按照4.2节的方法选择$$\alpha_2^k$$,求出新的$$\alpha_2^{new,unc}$$。$$\alpha_2^{new,unc} = \alpha_2^{k} + \frac{y_2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
3\)按照下式求出$$\alpha_2^{k+1}$$
$$\alpha_2^{k+1}= \begin{cases} H& {L \leq \alpha_2^{new,unc} > H}\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\ L& {\alpha_2^{new,unc} < L} \end{cases}$$
4\)利用$$\alpha_2^{k+1}$$和$$\alpha_1^{k+1}$$的关系求出$$\alpha_1^{k+1}$$
5\)按照4.3节的方法计算$$b^{k+1}$$和$$E_i$$
6)在精度e范围内检查是否满足如下的终止条件:
$$
\sum\limits_{i=1}^{m}\alpha_iy_i = 0
$$
$$
0 \leq \alpha_i \leq C, i =1,2...m
$$
$$
\alpha_{i}^{k+1} = 0 \Rightarrow y_ig(x_i) \geq 1
$$
$$
0 \leq \alpha_{i}^{k+1} \leq C \Rightarrow y_ig(x_i) = 1
$$
$$
\alpha_{i}^{k+1}= C \Rightarrow y_ig(x_i) \leq 1
$$
7\)如果满足则结束,返回$$\alpha^{k+1}$$,否则转到步骤2)。