RJW chap 11 visualisations notes (#12)

* Initial commit of Chap 3 notes

* Comment out package install and create new slide for meeting videos

* All slides up to the rabies example

* commit before presenting

* final tweak to slides

* final commit pre presentation

---------

Co-authored-by: lgibson7 <“[email protected]”>
Co-authored-by: Lydia Gibson <[email protected]>

Author: 3 people

07_techniques-for-machine-learning-applications.Rmd

@@ -1,24 +1,177 @@
 # Techniques for Machine Learning Applications
 
-**Learning objectives:**
+**Learning Objectives:**
 
-- THESE ARE NICE TO HAVE BUT NOT ABSOLUTELY NECESSARY
+-   How to manipulate data through feature engineering\
+-   Select the most suitable model for your data\
+-   Learn about machine learning algorithms
 
-## SLIDE 1 {-}
+## Goals of the Analysis and Nature of Data
 
-- ADD SLIDES AS SECTIONS (`##`).
-- TRY TO KEEP THEM RELATIVELY SLIDE-LIKE; THESE ARE NOTES, NOT THE BOOK ITSELF.
+### Output is *Continuous*
 
-## Meeting Videos {-}
+-   Example: How do explanatory variables such as lifestyle or chronic diagnoses affect LE / DALYs
+-   Traditional **regression models**, including linear regression (OLS), ridge & lasso
+-   Coefficient estimates quantify the association between changes in input and changes in outcome.
 
-### Cohort 1 {-}
+### Output is *Categorical* or *Binary*
+
+-   Outcome is categorical (e.g., disease/no disease)
+-   Can use logistic regression (more common for *explaining*)
+-   Or classification (more common for *predicting*)
+
+### Systemic Modelling / Simulation
+
+-   For complex systems modelled by multiple equations
+-   Typically more *predictive*
+-   Have a series of equations to fit to data, for example SIR model
+-   May wish to change parameters for sensitivity or explore how changes to inputs affects predicted outcome
+
+### Time-Series
+
+-   Data has a temporal or seasonal aspect (influenza?)
+-   Models like ARIMA can be used to model autocorrelation & trends
+
+## Statistical and Machine Learning Methods
+
+-   Several pre-analysis steps are common to many methods
+
+### Exploratory Data Analysis
+
+- Aim is to understand the data
+- Descriptive statistics of central tendencies and variation
+- Basic plots of distributions / skewness (histograms)
+- Correlation plots
+
+### Feature Engineering / Transforming Variables
+
+- Reducing skew (log or other transformation)
+- Encoding category variables as dummies
+- Creating new predictor variables, interaction terms
+- Centering / Scaling Variables
+
+## Case Study: Predicting Rabies
+
+### Goal:
+
+Predict DALYs due to rabies in 'Asia' and 'Global' regions, using the `hmsidwR::rabies` dataset
+
+### Exploratory Data Analysis (EDA)
+
+-   Dataset contains all cause and rabies mortality plus DALYs for the Asian and Global region, subdivided by year
+
+-   Values have an estimate and upper and lower boundaries in separate columns
+
+-   240 observations across 7 variables.
+
+-   Examining the data shows that death rates (`dx_rabies`) and DALYs (`dalys_rabies`) are different in magnitude and scale
+
+```{r rabiesdata, message=FALSE, warning=FALSE}
+
+library(tidyverse)
+rabies <- hmsidwR::rabies %>%
+  filter(year >= 1990 & year <= 2019) %>%
+  select(-upper, -lower) %>%
+  pivot_wider(names_from = measure, values_from = val) %>%
+  filter(cause == "Rabies") %>%
+  rename(dx_rabies = Deaths, dalys_rabies = DALYs) %>%
+  select(-cause)
+
+rabies %>% head()
+
+```
+
+-   After scaling, these values are closer together in magnitude, avoiding the issue of larger variables dominating others in prediction
+
+```{r}
+
+library(patchwork)
+
+p1 <- rabies %>%
+  ggplot(aes(x = year, group = location, linetype = location)) +
+  geom_line(aes(y = dx_rabies),
+            linewidth = 1) +
+  geom_line(aes(y = dalys_rabies))
+
+p2 <- rabies %>%
+  # apply a scale transformation to the numeric variables
+  mutate(year = as.integer(year),
+         across(where(is.double), scale)) %>%
+  ggplot(aes(x = year, group = location, linetype = location)) +
+  geom_line(aes(y = dx_rabies),
+            linewidth = 1) +
+  geom_line(aes(y = dalys_rabies))
+
+p1 + p2
+
+```
+
+### Training and Resampling
+
+-   The dataset was split into 80% training and 20% final test, stratified by location
+-   The 80% training set was then used to create a series of 'folds' or resamples of the data
+-   These folds can then be used to validate how well each model (and selected parameters) match unseen data
+-   K-fold cross validation was used to generate 10 folds using the `vfold_cv()` function from the tidymodels package
+
+### Preprocessing
+
+-   Handled using 'recipes' as part of tidymodels pipelines
+-   **Recipe 0** - all predictors, no transformations [reference model]
+-   **Recipe 1** - encoding of dummy variable for region, standardised numeric variables
+-   **Recipe 2** - as recipe 2, with addition of method to reduce skewness of `dalys_rabies` outcome
+-   Advantage of 'recipe' approach in tidymodels is that they can be piped / swapped out easily.
+
+### Multicollinearity
+
+-   DALYs & mortality likely to be strongly correlated (DALYs = Years_life_lost + Years_lived_w_disability))
+-   All cause and specific cause mortality also will have some correlation
+-   This can cause issues with some prediction methods, making it hard for the model to determine which variables have the best predictive power.
+-   In this analysis, dealt with by the choice of prediction method: Random forests and GLM with lasso penalty both robust to multicollinearity
+
+### Model 1: Random forest
+
+-   Specified using `rand_forest()` function within tidymodels framework
+-   Hyperparameters tuned using cross-validation and `tune_grid()` / grid search
+-   Optimal parameters gave RMSE 0.506
+-   Fig 7.4a shows close relationship between predictions and observed data
+
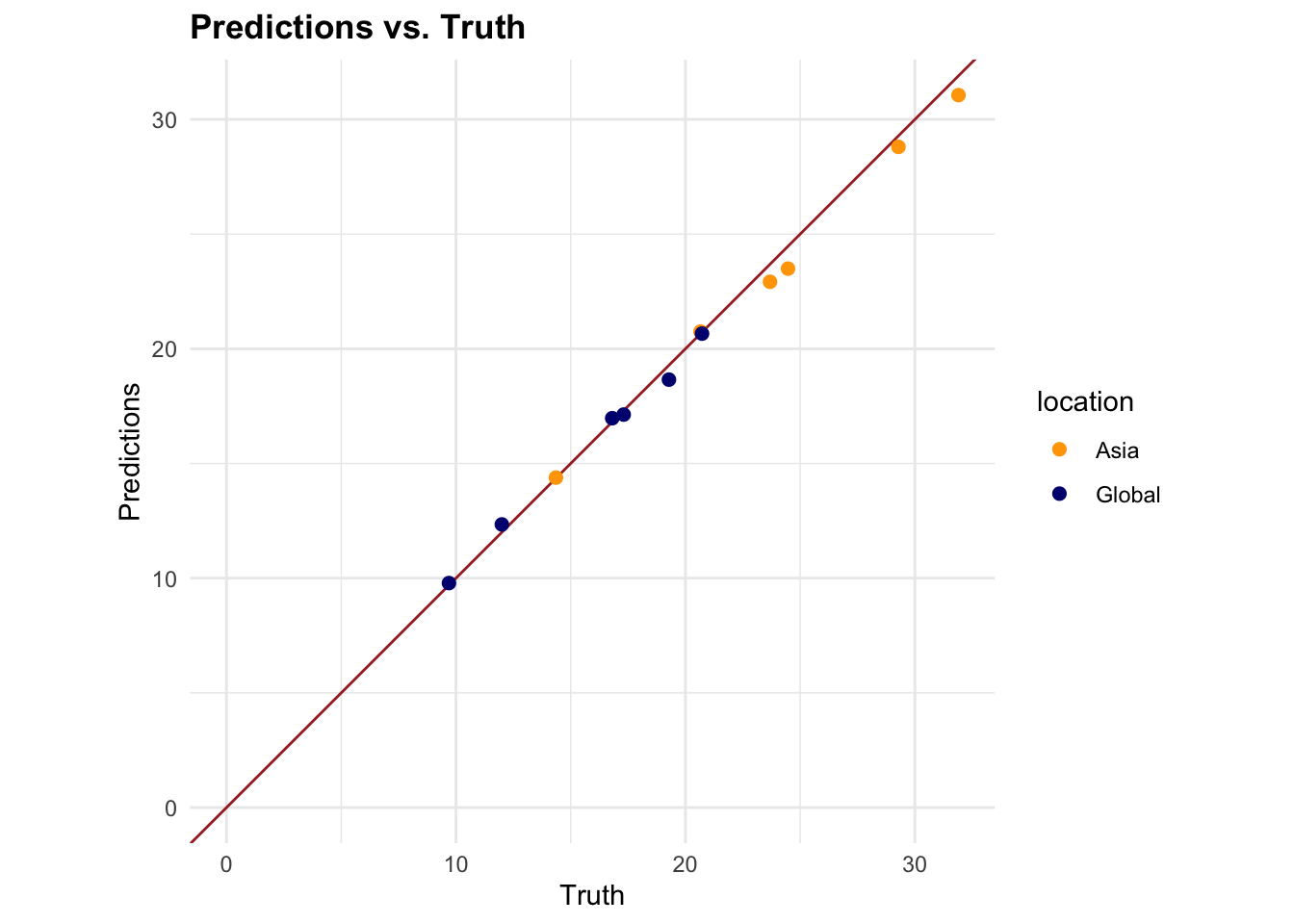+[![Fig 7.4a from chapter](https://fgazzelloni.quarto.pub/06-techniques_files/figure-html/fig-rf-predictions-1.png)](https://fgazzelloni.quarto.pub/06-techniques.html#fig-rf-predictions-1)
+
+### Model 2: GLM w lasso penalty
+
+- Generalised Linear Model with penalty term ($\lambda$)
+- Cross-validation process (as done for model 1) to tune $\lambda$ parameter
+- Results in lower RMSE than random forest
+
+### Additional models!
+
+- Last section showed code using `parsnip` package and `workflow_set()` to test more models
+- SVN with yeo_johnson transformation of output may actually improve on GLM (graded on RSME)
+
+## Summary
+
+This chapter focussed on ML techniques as a holistic analysis pipeline, not on individual ML algorithms or methods. Best practices are summarised at the end of the chapter:
+
+- Conduct exploratory data analysis to understand the underlying structure of the data and relationships between variables.
+- Apply feature engineering techniques to create new variables and enhance the model’s predictive power.
+- Select machine learning models that are contextually appropriate and robust for public health data analysis. Such as Random Forest, Generalised Linear Models, and others.
+- Use parameter calibration techniques such as cross-validation, regularisation, monte carlo, and grid search to optimise model performance.
+- Evaluate model performance using appropriate metrics and visualisation tools to assess predictive accuracy and relevance.
+
+TLDR: It's not just about applying the individual ML model but about considering the goals, dataset, preprocessing, calibration and evaluation of the model.
+
+## Meeting Videos {.unnumbered}
+
+### Cohort 1 {.unnumbered}
 
 `r knitr::include_url("https://www.youtube.com/embed/URL")`
 
 <details>
-<summary> Meeting chat log </summary>
 
-```
+<summary>Meeting chat log</summary>
+
+```         
 LOG
 ```
+
 </details>

11_interpreting-model-results-through-visualisation.Rmd

@@ -2,12 +2,119 @@
 
 **Learning objectives:**
 
-- THESE ARE NICE TO HAVE BUT NOT ABSOLUTELY NECESSARY
+ - Visualize predicted vs. observed values and assess residuals
+ - Interpret model metrics with VIP, accuracy, and partial dependency plots
+ - Create and customize ROC curves and compute AUC for classification models
 
-## SLIDE 1 {-}
 
-- ADD SLIDES AS SECTIONS (`##`).
-- TRY TO KEEP THEM RELATIVELY SLIDE-LIKE; THESE ARE NOTES, NOT THE BOOK ITSELF.
+
+## Why Plot Model Fits? {-}
+
+ - Single measures like MSE or $R^2$ can occasionally be misleading
+ 
+![Anscombe's Quartet - all 4 plots have the same linear model fit and R^2 but different input-output relationships ](https://upload.wikimedia.org/wikipedia/commons/thumb/e/ec/Anscombe%27s_quartet_3.svg/960px-Anscombe%27s_quartet_3.svg.png)
+ 
+
+## Predicted vs Actual Plots {-}
+
+ - Predicted vs Actual Plot: Scatter of model predictions vs observed values
+ - 45° line = perfect match of prediction and actual (very rare!)
+ - Near line = predictions close to true values (high accuracy)
+ - Far off line = larger errors, indicators performing less well
+ - Can reveals patterns of bias: e.g. consistent under-prediction or over-prediction
+
+<BR>
+
+![Example body fat prediction model](images/ch10-bodyfat_predicted_vs_actual.png)
+
+## Residual Plots {-}
+
+ - Residual = Actual – Predicted: measures error for each prediction
+ - Residual Plot: residuals on y-axis vs. predicted value or input on x axis
+ - Ideal outcome: Residuals normally distributed around 0 (no pattern)
+ - A pattern in residuals indicates model misspecification (e.g. curve suggests missing non-linear term)
+ - Heteroskedasticity: Residuals get bigger with x axis (fan shape), error variance isn’t constant and std errors may be wrong
+ - Can identify outliers: Large residuals may indicate points that distort or need investigating
+
+![Figure 11.6](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-meningitis-residuals-1.png)
+
+
+## Influential Observations {-}
+
+ - High-Leverage Point: An observation with extreme values (far from the average input/output)
+ - These points pull linear model fit disproportionately (can change slope/coefficients)
+ - High leverage + large residual = Influential outlier (can skew model)
+ - Can use diagnostics like Cook’s Distance (in stats package) to identify influential points
+ - Investigate high-leverage cases and consider fixes if needed
+
+```r
+
+library(RColorBrewer)
+
+data_pred |> 
+  mutate(cook_over_1 = cooks.distance(mod3) > 1) |> 
+  ggplot(aes(Deaths, Residuals, colour = cook_over_1)) +
+  geom_point() +
+  geom_hline(yintercept = 0, color = "red") +
+  scale_colour_manual(values = brewer.pal(3, "Set1")[1:2],
+                      labels = c("Cook's D ≤ 1", "Cook's D > 1"),
+                      name = "Influence") +
+  labs(title = "Residuals vs. Deaths due to COVID-19",
+       x = "Deaths", y = "Residuals")
+
+```
+
+![Points where Cook's Distance > 1](images/chap10_cook.png)
+
+## Comparing Models {-}
+
+ - Multiple Models Comparison: e.g. bar chart of R²/AIC for each model
+ - Actual vs Predicted with additional aesthetic or facet for each model
+ - Aids the choice of model / specification / hyperparameters
+ 
+![Previous Example - COVID-19 model](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-covid19_model-comparison-1.png)
+![Figure 11.5 from the book](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-meningitis-1.png)
+
+## Communicating Results {-}
+
+ - Some models conducive to clear visualisation, e.g. decision-tree model can be ploted with {rpart.plot}
+ - This sets out the fitted algorithmic choices and their effect on the predicted outputs
+
+![Fig 11.8: Decision tree for Ischaemic Stroke](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-dv-tree-1.png)
+
+ - Random forests can show variable importance plots
+ - These show the ranked importance of each predictive element
+ - Low ranking elements can be dropped if little effect on the model
+ 
+![Fig 11.9: Variable Importance for Ischaemic Stroke](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-rf-importance-1.png)
+
+ - Neither visualisation makes a *causal* claim, but can often give clues to make inferences.
+
+## ROC Plots {-}
+
+ - ROC curve = Sensitivity (True positive rate) vs. 1–Specificity (False Positive Rate) across all thresholds – shows the trade-off.
+ - AUC (Area Under Curve) is the overall performance indicator (1.0 = perfect, 0.5 = chance). Higher AUC = better model on average.
+ - Use ROC to pick a threshold that fits your needs: E.g., for initial diagnoses, you might choose a threshold giving high sensitivity (accepting more false positives to catch more true cases).
+ - If false positives are costly, pick a threshold with higher specificity (fewer false alarms, but you may miss some positives).
+ - Compare models with ROC/AUC: a higher AUC or a curve closer to the top-left means a stronger model.
+ 
+![Figure 11.10: ROC Curve for Ischaemic Stroke](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-roc-curve-1.png)
+
+## Partial Independence Plots {- }
+
+ - Plot how prediction / output changes with changes in one input
+ - **Assuming** other variables held constant (typically at average for the dataset)
+ - Can show marginal effects or key thresholds as the value of the input changes
+ - Need to be aware that assuming other variables don't change may not be realistic -
+    - inputs may be correlated 
+ 
+![Figure 11.11: Partial Dependence Plot](https://fgazzelloni.quarto.pub/10-applications_files/figure-html/fig-partial-dependence-1.png)
+
+## Conclusion {-}
+
+- Visualising the model helps evaluating the quality of the model specification
+- It can also be a boon to help communicate results to non-technical audiences
+- Visualisations can also assist in fine-tuning models and evaluating individual predictor effects
 
 ## Meeting Videos {-}