本题为代码随想录后续扩充题目,还没有视频讲解,顺便让大家练习一下ACM输入输出模式(笔试面试必备)
题目描述
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
输入描述
第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间,直至文件结束。
输出描述
输出每个指定区间内元素的总和。
输入示例
5
1
2
3
4
5
0 1
1 3
输出示例
3
9
数据范围:
0 < n <= 100000
本题我们来讲解 数组 上常用的解题技巧:前缀和
首先来看本题,我们最直观的想法是什么?
那就是给一个区间,然后 把这个区间的和都累加一遍不就得了,是一道简单不能再简单的题目。
代码如下:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, a, b;
cin >> n;
vector<int> vec(n);
for (int i = 0; i < n; i++) cin >> vec[i];
while (cin >> a >> b) {
int sum = 0;
// 累加区间 a 到 b 的和
for (int i = a; i <= b; i++) sum += vec[i];
cout << sum << endl;
}
} 代码一提交,发现超时了.....
我在制作本题的时候,特别制作了大数据量查询,卡的就是这种暴力解法。
来举一个极端的例子,如果我查询m次,每次查询的范围都是从0 到 n - 1
那么该算法的时间复杂度是 O(n * m) m 是查询的次数
如果查询次数非常大的话,这个时间复杂度也是非常大的。
接下来我们来引入前缀和,看看前缀和如何解决这个问题。
前缀和的思想是重复利用计算过的子数组之和,从而降低区间查询需要累加计算的次数。
前缀和 在涉及计算区间和的问题时非常有用!
前缀和的思路其实很简单,我给大家举个例子很容易就懂了。
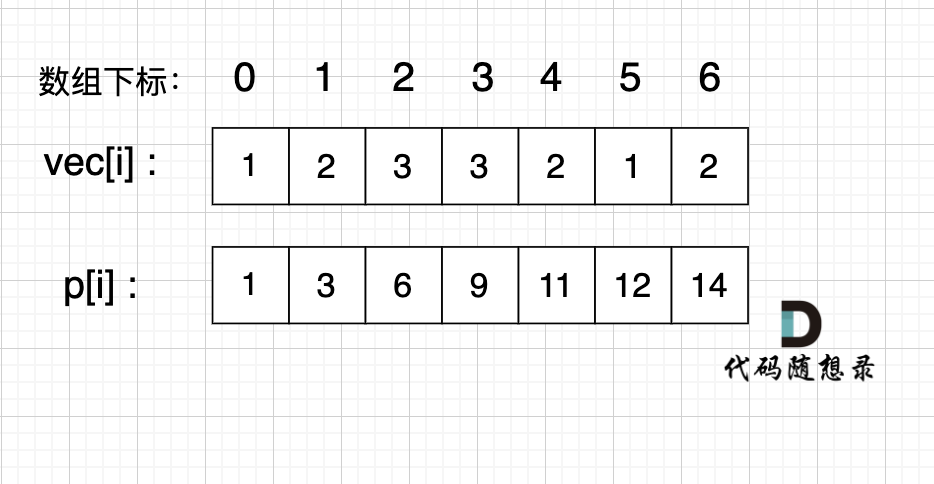
例如,我们要统计 vec[i] 这个数组上的区间和。
我们先做累加,即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和。
如图:
如果,我们想统计,在vec数组上 下标 2 到下标 5 之间的累加和,那是不是就用 p[5] - p[1] 就可以了。
为什么呢?
p[1] = vec[0] + vec[1];
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。
如图所示:
p[5] - p[1] 就是 红色部分的区间和。
而 p 数组是我们之前就计算好的累加和,所以后面每次求区间和的之后 我们只需要 O(1) 的操作。
特别注意: 在使用前缀和求解的时候,要特别注意 求解区间。
如上图,如果我们要求 区间下标 [2, 5] 的区间和,那么应该是 p[5] - p[1],而不是 p[5] - p[2]。
很多录友在使用前缀和的时候,分不清前缀和的区间,建议画一画图,模拟一下 思路会更清晰。
本题C++代码如下:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, a, b;
cin >> n;
vector<int> vec(n);
vector<int> p(n);
int presum = 0;
for (int i = 0; i < n; i++) {
cin >> vec[i];
presum += vec[i];
p[i] = presum;
}
while (cin >> a >> b) {
int sum;
if (a == 0) sum = p[b];
else sum = p[b] - p[a - 1];
cout << sum << endl;
}
}
C++ 代码 面对大量数据 读取 输出操作,最好用scanf 和 printf,耗时会小很多:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, a, b;
cin >> n;
vector<int> vec(n);
vector<int> p(n);
int presum = 0;
for (int i = 0; i < n; i++) {
scanf("%d", &vec[i]);
presum += vec[i];
p[i] = presum;
}
while (~scanf("%d%d", &a, &b)) {
int sum;
if (a == 0) sum = p[b];
else sum = p[b] - p[a - 1];
printf("%d\n", sum);
}
}
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] vec = new int[n];
int[] p = new int[n];
int presum = 0;
for (int i = 0; i < n; i++) {
vec[i] = scanner.nextInt();
presum += vec[i];
p[i] = presum;
}
while (scanner.hasNextInt()) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int sum;
if (a == 0) {
sum = p[b];
} else {
sum = p[b] - p[a - 1];
}
System.out.println(sum);
}
scanner.close();
}
}
import sys
input = sys.stdin.read
def main():
data = input().split()
index = 0
n = int(data[index])
index += 1
vec = []
for i in range(n):
vec.append(int(data[index + i]))
index += n
p = [0] * n
presum = 0
for i in range(n):
presum += vec[i]
p[i] = presum
results = []
while index < len(data):
a = int(data[index])
b = int(data[index + 1])
index += 2
if a == 0:
sum_value = p[b]
else:
sum_value = p[b] - p[a - 1]
results.append(sum_value)
for result in results:
print(result)
if __name__ == "__main__":
main()function prefixSum() {
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputLines = [];
rl.on('line', (line) => {
inputLines.push(line.trim());
});
rl.on('close', () => {
// 读取项数 n
const n = parseInt(inputLines[0]);
// 使用前缀和,复杂度控制在 O(1)
let sum = new Array(n);
sum[0] = parseInt(inputLines[1]);
// 计算前缀和数组
for (let i = 1; i < n; i++) {
let value = parseInt(inputLines[i + 1]);
sum[i] = sum[i - 1] + value;
}
// 处理区间和查询
for (let i = n + 1; i < inputLines.length; i++) {
let [left, right] = inputLines[i].split(' ').map(Number);
if (left === 0) {
console.log(sum[right]);
} else {
console.log(sum[right] - sum[left - 1]);
}
}
});
}
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
int num;
// 读取数组长度
scanf("%d", &num);
// 使用动态内存分配而不是静态数组,以适应不同的输入大小
int *a = (int *)malloc((num + 1) * sizeof(int));
// 初始化前缀和数组的第一个元素为0
a[0] = 0;
// 读取数组元素并计算前缀和
for (int i = 1; i <= num; i++)
{
int mm;
scanf("%d", &mm);
// 累加前缀和
a[i] = a[i - 1] + mm;
}
int m, n;
// 循环读取区间并计算区间和,直到输入结束
// scanf()返回成功匹配和赋值的个数,到达文件末尾则返回 EOF
while (scanf("%d%d", &m, &n) == 2)
{
// 输出区间和,注意区间是左闭右开,因此a[n+1]是包含n的元素的前缀和
printf("%d\n", a[n+1] - a[m]);
}
// 释放之前分配的内存
free(a);
return 0;
}