Skip to content

Latest commit

 

History

History
166 lines (119 loc) · 6.24 KB

positionalencoding.md

File metadata and controls

166 lines (119 loc) · 6.24 KB

1. 核心作用

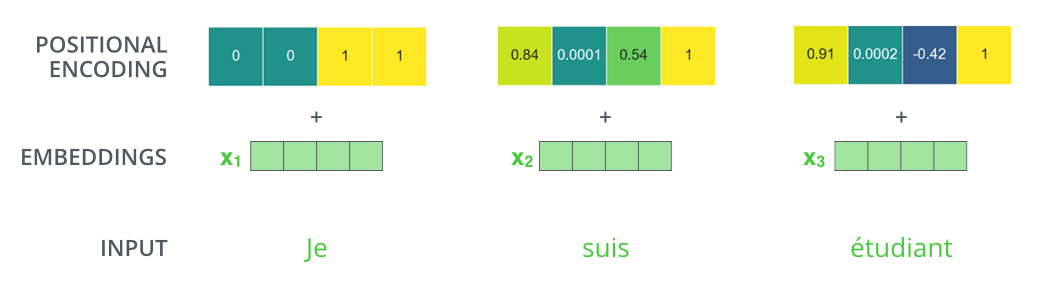
  • 注入序列顺序信息：由于Transformer的自注意力机制本身不具备感知词序的能力，需通过位置编码为每个位置生成独特的标识。
  • 处理变长序列：支持模型处理训练时未见过的序列长度（得益于正弦/余弦函数的周期性）。

2. 数学公式推导

2.1 基本公式

对于位置 $pos$和维度索引 $i$，位置编码的计算公式为：

$$\begin{aligned} PE_{(pos, 2i)} &= \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \\\ PE_{(pos, 2i+1)} &= \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right) \end{aligned}$$
2.2 公式解析
  • 频率控制：不同维度对应不同的波长（高频→捕捉局部位置，低频→捕捉全局位置）
    • 维度索引$i$越大，分母指数$\frac{2i}{d_{\text{model}}}$越大 → 频率越低
  • 奇偶交替：偶数维度用正弦，奇数维度用余弦（确保相邻维度相关性）
2.3 波长计算示例

假设 $d_{\text{model}}=512$：

  • 当 $i=0$时，波长： $10000^{0/512}=1$ → 周期为 $2\pi$
  • 当 $i=255$时，波长： $10000^{510/512}≈10000^{0.996}≈9540$ → 周期极长

3. 代码实现（PyTorch）

import torch
import torch.nn as nn
import math

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        super().__init__()
        
        # 生成位置编码矩阵 [max_len, d_model]
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)  # [max_len, 1]
        
        # 计算div_term：10000^(2i/d_model)的倒数（对数空间计算避免溢出）
        div_term = torch.exp(
            torch.arange(0, d_model, 2).float() * 
            (-math.log(10000.0) / d_model
        )  # [d_model/2]
        
        # 填充偶数和奇数维度
        pe[:, 0::2] = torch.sin(position * div_term)  # 偶数维度：sin(pos/10000^(2i/d))
        pe[:, 1::2] = torch.cos(position * div_term)  # 奇数维度：cos(pos/10000^(2i/d))
        
        # 注册为缓冲区（不参与训练）
        self.register_buffer('pe', pe.unsqueeze(0))  # [1, max_len, d_model]
        
    def forward(self, x):
        """
        x: 输入张量 [batch_size, seq_len, d_model]
        返回: [batch_size, seq_len, d_model]
        """
        return x + self.pe[:, :x.size(1)]  # 自动广播相加

4. 代码与公式对应解析

公式步骤 代码实现
初始化位置矩阵 $PE$ pe = torch.zeros(max_len, d_model)
计算位置序列 $pos$ position = torch.arange(0, max_len).unsqueeze(1)
计算频率项 $\frac{1}{10000^{2i/d}}$ div_term = torch.exp(...) （对数变换避免数值溢出）
填充正弦项（偶数维度） pe[:, 0::2] = torch.sin(position * div_term)
填充余弦项（奇数维度） pe[:, 1::2] = torch.cos(position * div_term)
与输入相加 return x + self.pe[:, :x.size(1)]

5. 关键特性分析

5.1 相对位置感知能力

通过三角函数加法公式可推导相对位置关系：

$$\begin{aligned} PE_{pos+\Delta} &= \sin\left(\omega_k (pos+\Delta)\right) \\\ &= \sin(\omega_k pos)\cos(\omega_k \Delta) + \cos(\omega_k pos)\sin(\omega_k \Delta) \end{aligned}$$

其中 $\omega_k = 1/10000^{2k/d}$，表明相对位置 $\Delta$可通过线性变换表示。

5.2 可视化示例

位置编码热图

  • 纵轴：位置（0~50）
  • 横轴：维度（0~511）
  • 颜色：编码值（-1~1）

6. 设计优势

特性 说明
可扩展性 能处理比训练时更长的序列（如训练时max_len=5000，推理时处理6000长度）
确定性生成 无需学习参数，节省模型容量
各向异性编码 不同维度对应不同频率，编码空间更丰富
平移不变性 相邻位置的编码变化平滑，利于模型捕捉局部关系

7. 应用示例

# 参数设置
d_model = 512
max_len = 50
batch_size = 2
seq_len = 20

# 实例化模块
pe = PositionalEncoding(d_model)

# 模拟输入词向量
x = torch.randn(batch_size, seq_len, d_model)

# 添加位置编码
x_pe = pe(x)  # [2, 20, 512]

# 检查编码值
print(x_pe[0, 0, :4])  
# 示例输出：tensor([ 0.8415,  0.5403, -0.0042,  0.9999, ...])

8. 后续改进方案

类型 方法 特点
学习式位置编码 BERT、GPT 通过可训练参数学习位置嵌入，灵活性高但无法外推
相对位置编码 Transformer-XL 编码相对位置距离而非绝对位置，提升长文本处理能力
旋转位置编码 RoFormer 通过复数空间旋转操作编码位置，理论性质更优
混合编码 T5 前128维用学习式编码，后384维用固定式编码

9. 常见问题解答

Q1: 为什么不用简单的位置序号（如0,1,2,…）直接输入模型？

  • 答案：整数值缺乏可学习的语义信息，且会导致数值范围差异过大（如长序列中位置号远大于词向量值）。

Q2: 位置编码是否需要参与反向传播训练？

  • 原论文方案：固定不可训练（如代码中的register_buffer）。
  • 变体方案：可设置为可训练参数（如BERT）。

Q3: 如何处理超过max_len的序列？

  • 截断法：取最后max_len个位置
  • 外推法：按公式计算新位置编码（仅适用于正弦编码）