CPP-Sudoku-Solver

C++ Sudoku Solver using BackTrack technique.

Sudoku

Desciption

It is a logic-based, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called "boxes", "blocks", or "regions") contain all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.
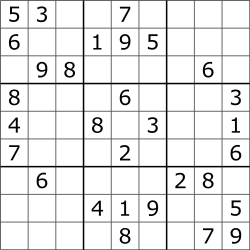
Example from Wikipedia (grid is here):

and solution (from SudokuSolver) is:

Constraints

For each row, column and subgrid all 9 cells are uinque (i.e. there're no two cells with same number). Sudoku grid has 9 subgrids; Subgrid is 3×3 grid you can see in the image below (indexed from (0, 0) to (2, 2) inclusive inside the main grid):

How to solve

• First, we determine the domain for each cell in the grid. Initially, all cells has domain from 1 to 9 inclusive but for example: if the row of cell has cells {1, 3, 8, 9}, its column has cells {1, 5, 7, 8} and its subgrid has {1, 2, 3, 5, 7, 8, 9} values then the cell can't have any of {1, 2, 3, 5, 7, 8, 9} which means its domain is {4, 6}.
• After setting the domains, for each cell we set its value from its domain and if there's no conflict between it and its neighboring cells (cells sharing row, col or subgrid) move to set the remaining unassigned cells if not reset this cell and try the next value from cells' domain. Keep repeating this process untill the grid is complete. That's a BackTracking approach!

Code Logic and Walkthrough

There're 2 main classes:

SudokuGrid

It represents a 9×9 grid structured as Variables and has utility for state validation, completeness checking and organizing input-output stuff

Var class

Var represents a cell on the grid which has current value and domain of values can represent.

Domain class

Instead of std::vector which has a length placeholder of 64-bit size and 8-bit for each possible value in the domain of a Var leading to allocate 64 bit for size + 8 bit * 9 (all possible domain values) = 136 bit for a single Var domain, I optimized that a little by bit flags (you can see this if unfamiliar to you) just for 16-bit size (8.5 better than using std::vector. just for this problem of course) with ability to push, pop or checking existence (via has method) of values.

Solver

It's just application of this logic such having:

• set_domains method:
  1. Extract taken values for each row, column, subgrid.
  2. For each Var (cell); its domain will be all values that's not in its row, column or subgrid (cell[i] = {1 : 9} - (cell[i]'s row ∪ cell[i]'s column ∪ cell[i]'s subgrid))
• backtrack method:

Function backtrack():
    if grid is complete:
        return true
    cell ← select_unassigned_cell()
    for each value in cell's domain:
        cell ← value
        if there's no conflict between cell and its neighboring cells:
            result ← backtrack()
            if result is true:
                return true
        else:
            reset cell
    return false

Run

After compiling files (for Ex.: g++ SudokuGrid.cpp SudokuSolver.cpp main.cpp -o main) and run exe file:

• for grids/0.txt (.\main grids/0.txt) you will be able to see:

Material

I got grids from dimitri/sudoku.