new doc about ibst

docs/Algorithm/implicit_BST.mdx

@@ -0,0 +1,145 @@
+---
+title: 隐式二叉搜索树 (implicit BST)
+description: 隐式二叉搜索树的原理\实现\优势\劣势
+tags: [algorithm, code, bioinfo]
+sidebar_position: 7
+---
+
+import ReferenceList from "@site/src/components/ReferenceList";
+import wikipedia from "@site/static/img/icon/wikipedia.png";
+
+## 背景
+
+Erik: https://github.com/pangenome/impg
+
+lh3: https://github.com/lh3/bedtk
+
+两位重量级都提到了这个概念，必须要学习一下。而且听起来也很高端的样子。
+
+
+## 定义
+
+### 隐式数据结构
+
+维基百科定义：
+
+> In computer science, an implicit data structure or space-efficient data structure is a data structure that stores very little information other than the main or required data: a data structure that requires low overhead. They are called "implicit" because the position of the elements carries meaning and relationship between elements; this is contrasted with the use of pointers to give an explicit relationship between elements.
+
+TL;DR: 隐式数据结构是一种空间高效，低开销的数据结构，为什么叫隐式，因为元素的位置本身就包含了元素之间的关系，而不是通过指针来明确元素之间的关系。
+
+乍一听，是乍一听的感觉。
+
+### 二叉搜索树
+
+这个老面孔了，简单的说：
+
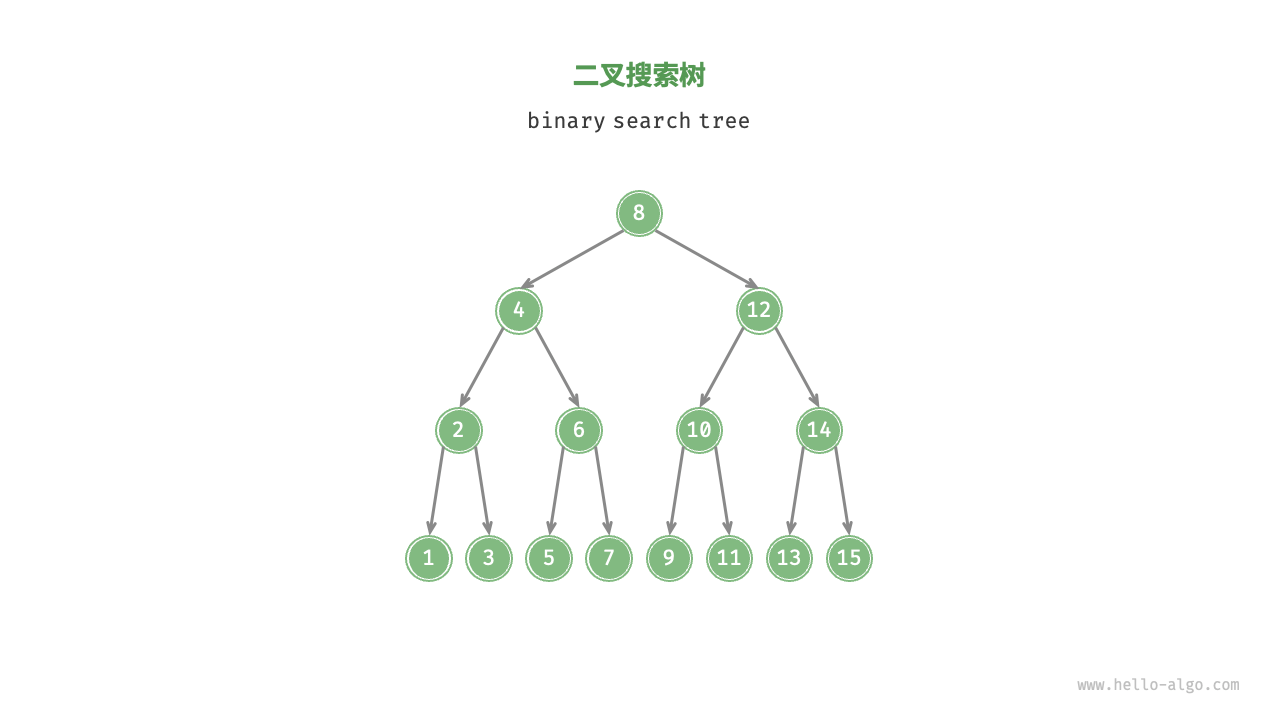
+二叉搜索树（binary search tree）满足以下条件。
+
+1. 对于根节点，左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。
+2. 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1。
+
+如下图所示，这样的特性是为了检索方便。
+
+![bst](https://www.hello-algo.com/chapter_tree/binary_search_tree.assets/binary_search_tree.png)
+
+具体的检索过程是，假定要查找的值为 $x$，从根节点开始，如果 $x$ 小于当前节点的值，则在左子树中查找，否则在右子树中查找，直到找到为止。
+
+### 隐式二叉搜索树
+
+Q: 我们真的需要用树结构来存储一个 BST 吗？
+
+A: 不用，可以用隐式数据结构来代替。
+
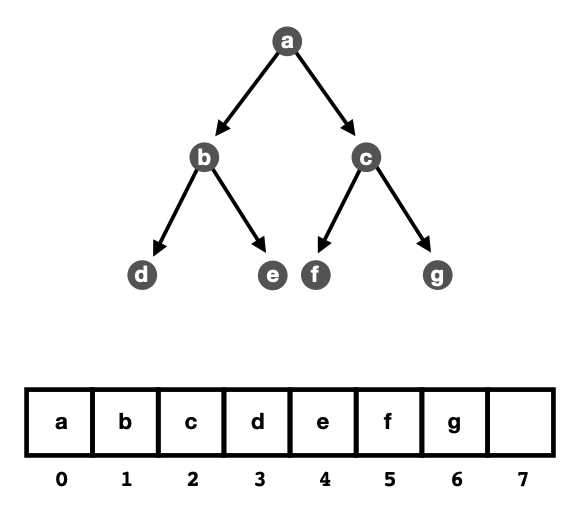
+具体而言，我们可以用一个排序好的数组来代替二叉搜索树，这样就不需要额外的指针来存储左右子树的信息了。
+其中数组的下标就是节点的位置，节点的值就是数组的值。如下图所示：
+
+![ibst](https://raw.githubusercontent.com/wjwei-handsome/wwjPic/main/img/20240825143026.png)
+
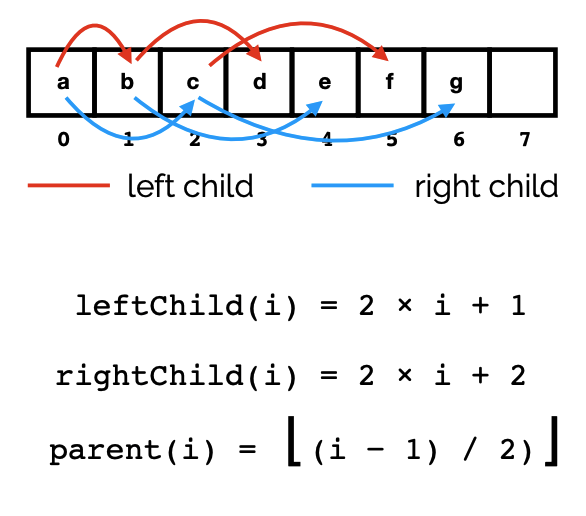
+左右子节点，有不同的索引下标，具体如图所示：
+
+![ibst_idx](https://raw.githubusercontent.com/wjwei-handsome/wwjPic/main/img/20240825143155.png)
+
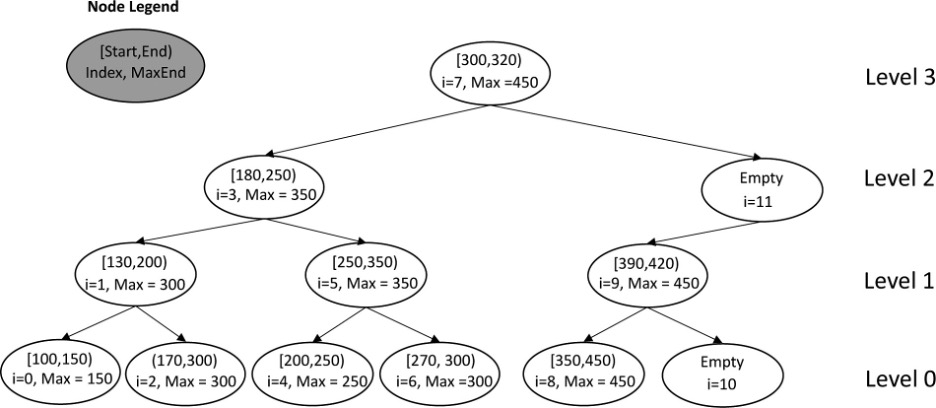
+lh3 那篇 bedtk 的文章也阐述地很清楚：
+
+![bedtk](https://raw.githubusercontent.com/wjwei-handsome/wwjPic/main/img/20240825143605.png)
+
+在这个例子中，BST 总共有 3 层，第一个根节点的索引就是$2^{3}-1=7$，左子节点的索引是$7-2^{3-1}$，右子节点的索引是$7+2^{3-1}$。以此类推。
+
+## 优势
+
+1. **空间高效：** 数组实现，不需要存储指针或引用。
+2. **缓存：** 由于数组是连续存储的，可以利用 CPU 缓存的特性，提高检索效率。
+3. **简单：** 结构简单，实现容易
+
+## 劣势
+
+1. **灵活性差：** 由于数组是连续存储的，插入删除操作需要移动大量元素，代价太大。
+2. **场景有限：** 适用于静态数据集，不适用于动态数据场景。
+
+## 实现
+
+这里仅实现了一个简单的隐式二叉搜索树的检索过程，省略了隐式数组的生成，具体代码如下：
+
+```rust
+struct ImplicitBST {
+    data: Vec<i32>, // 数组存储 BST
+}
+
+impl ImplicitBST {
+    pub fn new(data: Vec<i32>) -> Self {
+        ImplicitBST { data }
+    }
+
+    pub fn search(&self, value: i32) -> Option<usize> {
+        let mut idx = 0;
+        while idx < self.data.len() {
+            if self.data[idx] == value {
+                return Some(idx);
+            } else if self.data[idx] > value {
+                idx = 2 * idx + 1; // 左子节点
+            } else {
+                idx = 2 * idx + 2; // 右子节点
+            }
+        }
+        None
+    }
+}
+
+fn main() {
+    let ibst = ImplicitBST::new(vec![10, 5, 15, 3, 7, 12, 18]); // 已经排序好的数组，第一个节点为根节点，左节点索引为 2*i+1, 右节点索引为 2*i+2
+    // 因此这个例子的树结构为：
+    //         10
+    //        /  \
+    //       5    15
+    //      / \   / \
+    //     3   7 12 18
+
+    println!("Search for 7: {:?}", ibst.search(7)); // Output: Some(4)
+    println!("Search for 3: {:?}", ibst.search(3)); // Output: Some(3)
+    println!("Search for 20: {:?}", ibst.search(20)); // Output: None
+}
+```
+
+## impg 的原理
+
+据我所知，impg 设计的初衷是不想构建整个完整的 graph, 因为由于种种原因，完整的 pan-graph 会变得很复杂。一个解决方法是获得指定区间的子图，也就是指定区间的比对信息。
+
+具体而言，构建 pan-graph 的前期，会对每个基因组进行两两之间的 all-vs-all 比对，那么每个基因的比对信息，其实就是一组区间。
+
+用户指定一个基因组的区间，impg 就会去找每个 alignments 上有交集的区间，对于找到的交集区间，再重复上述过程，直到找到所有的区间。
+
+这样找到的比对信息，是一个找 [传递闭包](./transitive_closure.mdx)的过程，也就是说，如果 A 和 B 有比对信息，B 和 C 有比对信息，那么 A 和 C 也有比对信息。
+
+这样，就完成了一个 sub-graph 的检索，这样的操作也会 more flexible, parallelizable, and scalable.
+
+## 参考
+
+<ReferenceList
+    data={[
+        {
+            title: "维基百科",
+            link: "https://en.wikipedia.org/wiki/Implicit_data_structure",
+            src: wikipedia,
+        },
+    ]}
+/>